コンデンサとは
コンデンサは、導体と静電気の特徴を活かし、導体の表面に電荷を蓄えるよう工夫された部品です。
直流回路、交流回路のどちらにもよく使用されます。
直流回路ではノイズ除去や、電源電圧の安定。
交流回路では電力回路では力率改善に使用され、小信号回路ではフィルター、位相調整、積分回路等幅広く使用されます。
様々な所で応用され、非常に重要な部品です。本ページでは、コンデンサに関連する情報についてまとめました。
公式一覧
コンデンサに関連する公式をまとめると次の通りです。
電界の式(ガウスの法則) \(\displaystyle E=\frac{Q}{ε_0S}\)
電位と電界の関係式 \(V=Ed\)
蓄えられる電荷量・静電容量・電位の関係式 \(Q=CV\)
静電容量の式 \(\displaystyle C=ε\frac{S}{d}\)
静電エネルギーの式 \(\displaystyle U=\frac{1}{2}CV^2\)
2つのコンデンサを直列接続したときの合成の静電容量\(C[F]\)
\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
2つのコンデンサを並列接続したときの合成の静電容量\(C[F]\)
\(\displaystyle C=C_1+C_2\)
電界強度\(E[V/m]\)
電界強度Eの大きさ(ガウスの法則)
コンデンサの電界強度\(E[V/m]\)は
\(\displaystyle E=\frac{Q}{ε_0S}\)
コンデンサの電界強度\(E[V/m]\)の式の証明
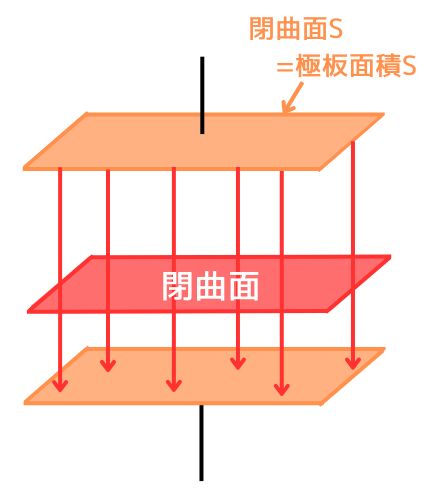
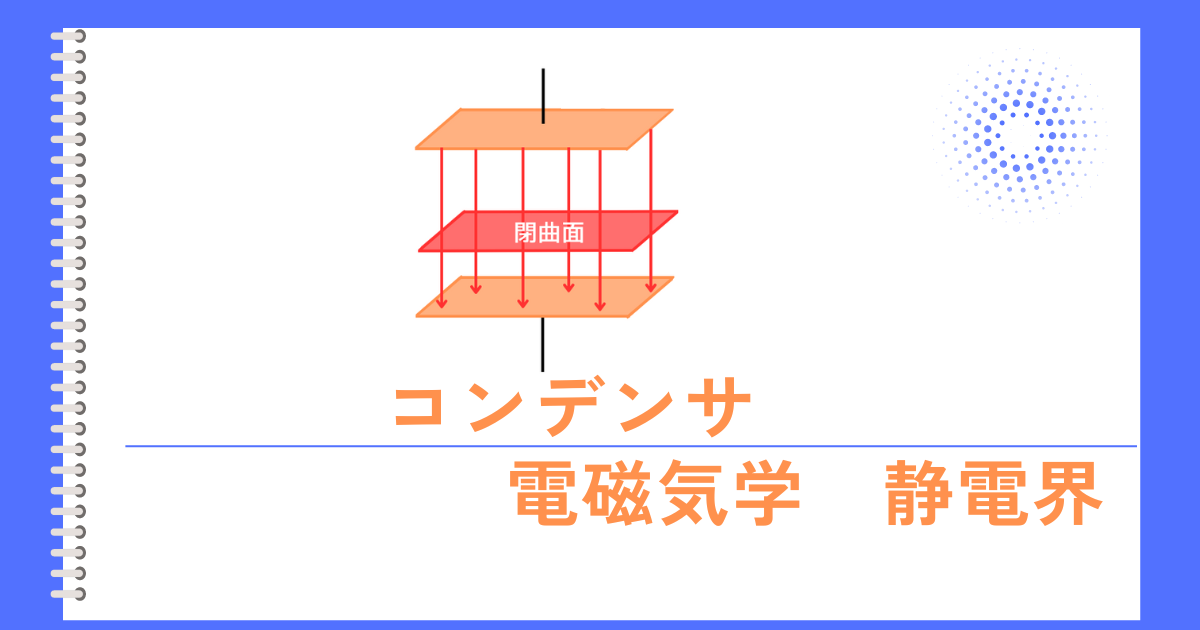
ガウスの法則の式を示します。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
平行平板コンデンサの極板間の電気力線は広がりませんので、閉曲面Sは、極板の表面となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、極板面積Sで一定ですので、
\(\displaystyle E=\frac{Q}{ε_0S}\)
となります。
コンデンサの電界分布
電界分布とは、電界強度\(E\)が場所によってどのように変化するかを示したものです。
電圧V[V]が与えられているときの電界分布
コンデンサの両端に電圧\(V[V]\)の直流電源を接続したとき、電界強度\(E\)をグラフにすると、常に一定の値\(\displaystyle E=\frac{V}{d}\)を示すグラフになります。
このとき、\(\displaystyle E=\frac{Q}{εS}\)の式はありますが、コンデンサの誘電率\(ε[F/m]\)が変わったとしても、電界強度\(E\)の大きさは変わらず一定です。(誘電率に依存しない)
コンデンサの電界分布が一定な理由
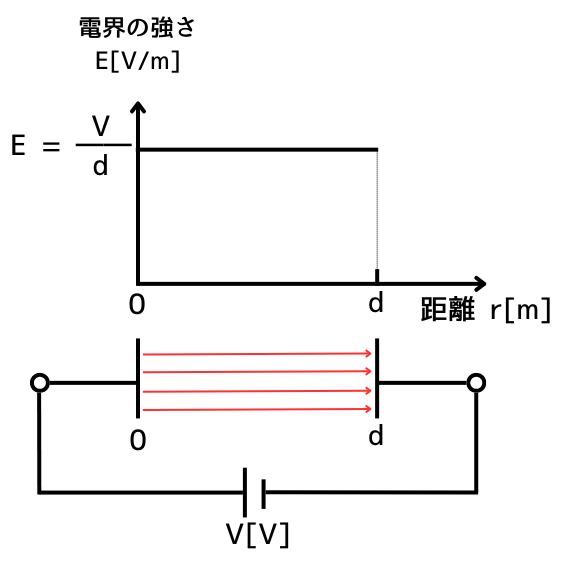
コンデンサの電界分布が一定な理由は、コンデンサの極板の表面から垂直に出た電気力線が、向かい合わせとなっているもう片方の極板に全て入るためです。
このことから、コンデンサの極板間の電界は、一様な電界
\(\displaystyle E=\frac{V}{d}\)
となります。
これをグラフに表すと左図の通りとなります。
電界強度\(E\)が誘電率\(ε\)に依存しない理由
電圧\(V\)が直流電源から与えられているときの電荷\(Q\)は次のように式を展開できます。したがって、電荷\(Q\)は電圧\(V\)に比例して変わります。
\(\displaystyle Q=CV=ε\frac{S}{d}V\)
電界強度の式に代入すると、
\(\displaystyle E=\frac{Q}{εS}=\frac{V}{d}\)
したがって、\(\displaystyle E=\frac{V}{d}\)となり、誘電率\(ε\)に依存しないことが示されました。
直列接続されているときの電界分布
異なる誘電率\(ε\)の誘電体を持つコンデンサを直列接続し、その両端に電圧\(V[V]\)の直流電源を接続したとき、電界強度\(E\)をグラフにすると、
\(\displaystyle E=\frac{Q}{εS}\)
の電界強度グラフになります。
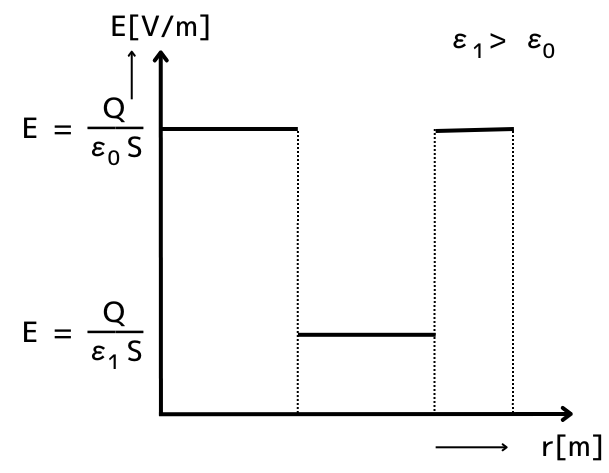
このとき、コンデンサの誘電率\(ε[F/m]\)の大きさに反比例して、電界強度\(E\)の大きさは変わります。
電界強度\(E\)が誘電率\(ε\)に依存する理由
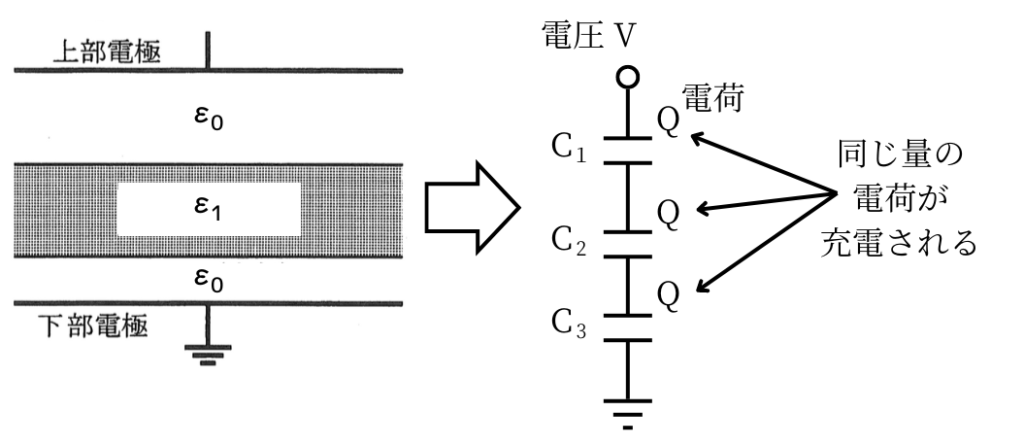
左図のように、誘電率\(ε_0\)の真空のコンデンサの間に誘電率\(ε_1\)の誘電体を挿入したとします。
このとき、コンデンサの各層(真空層・誘電体層)は直列接続されたものとみなせます。
直列接続されたコンデンサの両端に電圧\(V\)の直流電圧を与えた時、すべてのコンデンサに、同じ量の電荷\(Q\)が蓄えられます。
電界強度の式は、\(\displaystyle E=\frac{Q}{εS}\)であり、
各コンデンサの電荷量が一定であることから、電界強度は誘電率\(ε\)に反比例することがわかります。
以上より、異なる誘電率\(ε\)の誘電体を持つコンデンサを直列接続し、その両端に電圧\(V[V]\)の直流電源を接続したとき、誘電率\(ε\)に依存することが示されました。
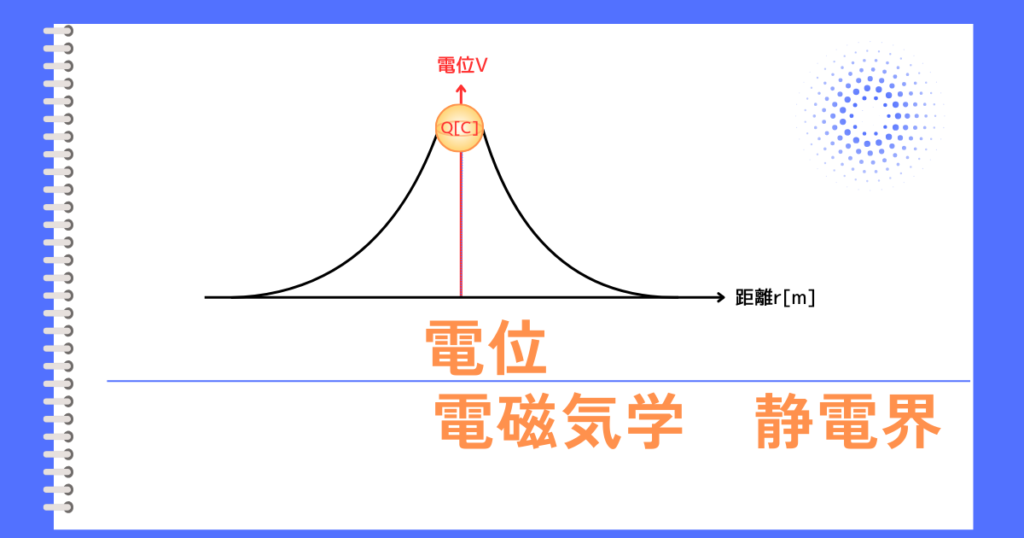
電位\(V[V]\)
平行平板コンデンサの一様な電界\(E[V/m]\)の場における電位\(V[V]\)は、極板間距離\(d[m]\)を使用し、次式で表されます。
\(V=Ed\)
電位\(V[V]\)の式の導出
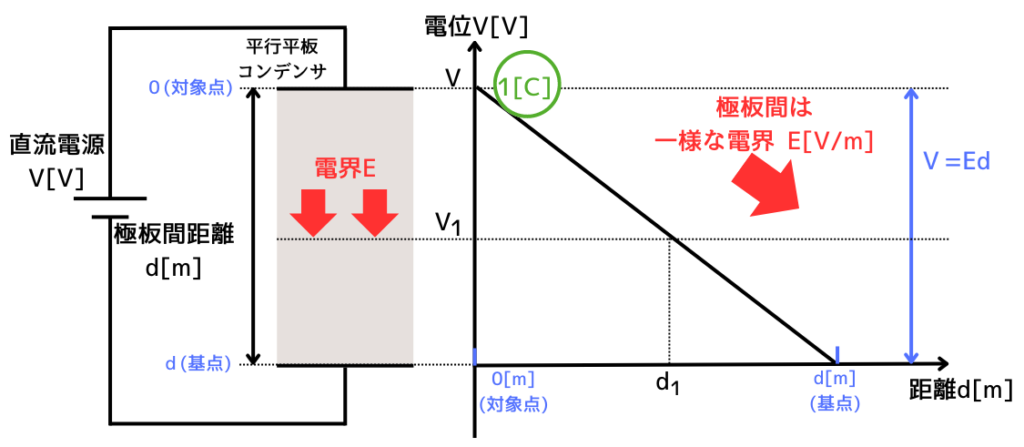
線電荷の作る電界の電界強度\(E[V/m]\)は、ガウスの法則から、(→ガウスの法則解説)
\(\displaystyle E=\frac{Q}{ε_0S}[V/m]\) …①
※Sは極板面積です。
この電界中で、単位電荷\(1[C]\)を基点から対象点まで移動させたときの電位を求めます。
このとき、コンデンサの極板間距離\(d[m]\)なので、
・基 点:\(d[m]\)
・対象点:\(0[m]\)
とします。
電位\(V[V]\)と電界\(E[V/m]\)の関係式は次の②式です。(→②式の解説ページ)
\(V=-\int_{基点}^{対象点}E dr\) …②
②式に①式を代入すると、
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{d}^{0}\frac{q}{ε_0S} dr = \frac{q}{ε_0S}\left[ r \right]_0^d \\
&=& \frac{q}{ε_0S}(d-0) = \frac{q}{ε_0S}d=Ed
\end{eqnarray}\)
以上、\(\displaystyle V=Ed\)が導出できました。
平行平板コンデンサの等電位面
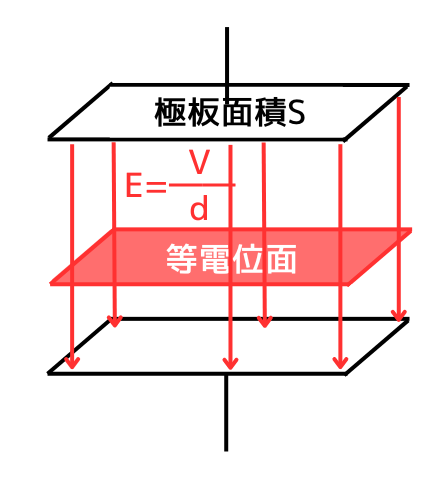
平行平板コンデンサの電界\(E[V/m]\)の項目に示した通り、極板間の電界の強さ\(E\)は、どこでも同じ強度です。
そのため、
\(V=Ed\)で示される電位は、極板の形と同じ形となります。
つまり、電極板と誘電体の境界面に対して平行といえます。
電荷量\(Q[C]\)
電荷量\(Q[C]\)が\(1C\)で電位差\(V[V]\)が\(1V\)の場合、静電容量\(C[F]\)は\(1F\)と定められています。このことから、コンデンサに蓄えられる電荷量・静電容量・電位の関係式は、次式で表されます。
\(Q=CV[C]\)
\(Q=CV\)のイメージ
電荷量\(Q[C]\)・静電容量\(C[F]\)・電位\(V[V]\)の関係は水槽に溜められた水と比較すると、イメージしやすいかと思います。
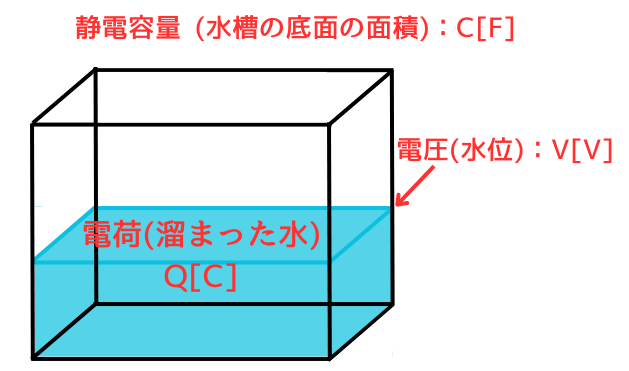
コンデンサは電荷\(Q[C]\)を蓄える水槽として考えると、静電容量\(C[F]\)は水槽の容量です。
コンデンサに蓄えられる電荷\(Q\)は、\(Q=CV[C]\)
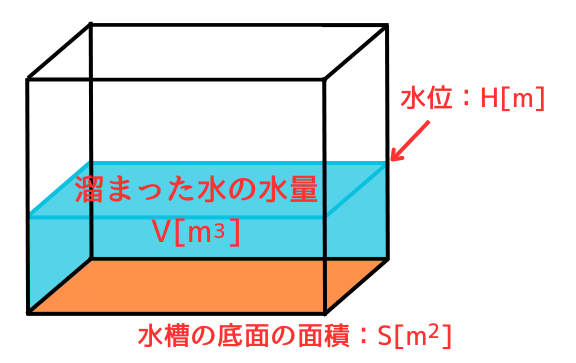
水槽に溜められる水は、\(V=SH\)であることから、
・電荷\(Q[C]\)は、水量\(V[m^3]\)
・静電容量\(C[F]\)は、水槽の面積\(S[m^2]\)
・電位\(V[V]\)は、水位\(H[m]\)
と、対応します。
この対応を絵にすると、下図のようになります。
静電容量\(C[F]\)
静電容量の式 \(\displaystyle C=ε\frac{S}{d}\)
静電容量\(C[F]\)の式の証明
コンデンサの電位と電界関係から、
\(V=Ed\) ………①
コンデンサの電界強度\(E\)(ガウスの法則)から、
\(\displaystyle E=\frac{Q}{εS}\) ………②
電荷Q・静電容量C・電位Vの関係式から、
\(Q=CV\)
⇔ \(\displaystyle C=\frac{Q}{V}\) ………③
③式に①・②式を代入していくと、次のように展開できます。
\(\displaystyle C=\frac{Q}{V}=\frac{Q}{Ed}=\frac{Q}{\frac{Q}{ε_0S}d}=ε_0\frac{S}{d}\)
以上より、\(\displaystyle C=ε_0\frac{S}{d}\)が求められました。
蓄えられる静電エネルギー\(U[J]\)
静電エネルギー\(U[J]\)の式
\(\displaystyle U=\frac{1}{2}CV^2[J]\)
静電エネルギー\(U[J]\)の式の導出
①
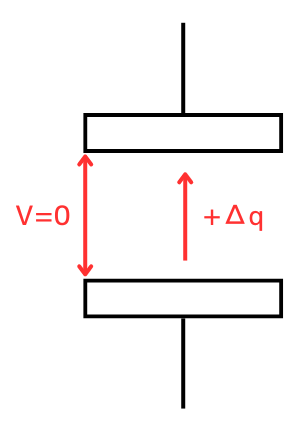
電位が\(V\)だけ大きいところに微小電荷\(Δq\)を動かすには、\(Δq・V\)の仕事が必要になります。
コンデンサ内に電荷が無い時、\(Δq\)を移動させるエネルギーは、\(V=0[V]\)なので、必要な仕事量\(ΔW_0=0[J]\)です。
②
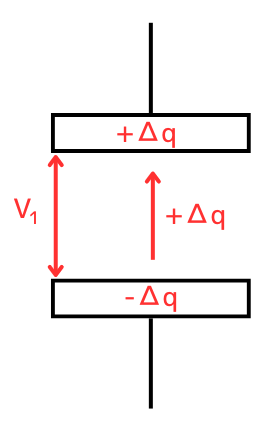
しかし、電荷を移動させていくと、\(\displaystyle V=\frac{q}{C}\)の関係から、電位差も大きくなっていきますので、必要な仕事量が増加していきます。
\(Δq\)が移動し、コンデンサの電位が\(V_1[V]\)になった時、次に\(Δq\)を移動させるエネルギーは、\(ΔW_1=ΔqV_1\)です。
③
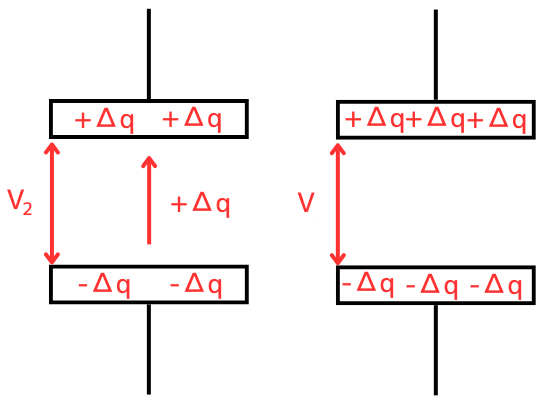
\(Δq\)が移動し、コンデンサの電位が\(V_2[V]\)になった時、次に\(Δq\)を移動させるエネルギーは、\(ΔW_2=ΔqV_2\)と大きくなっていきます。
最終的に、電位\(V[V]\)になったとき、
電荷の移動がなくなったとします。
④
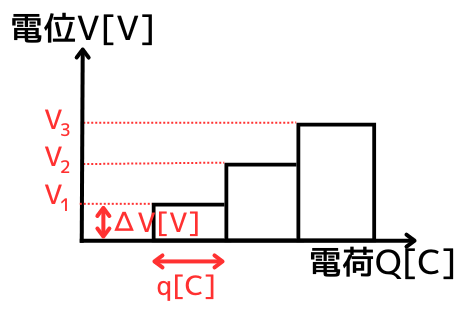
今までの微小電荷\(q[C]\)の溜まりと、コンデンサの電位\(V[V]\)の変化をグラフにすると、左図のようになります。
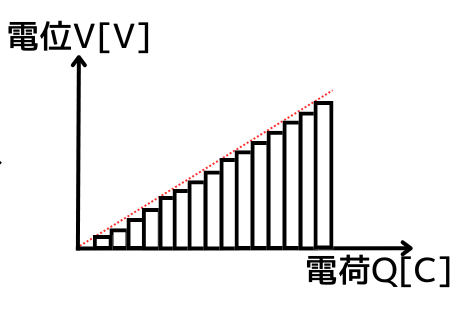
⑤
横軸をもっと細かくしていくと、直線グラフを描くことができます。
コンデンサは、\(q=0\)から、\(q=Q\)まで電荷を蓄えるので、
微小電荷が移動するエネルギー
\(ΔW=ΔqV\)
の式を、コンデンサに蓄えられた電荷が\(Q=0[C]\)から、\(Q=Q[C]\)になるまで積分すると、コンデンサに蓄えられる静電エネルギーが求められます。
⑥
積分をして静電エネルギーの式を求めます。
電位Vの式は、\(q=CV\) ⇔ \(\displaystyle V=\frac{q}{C}\)です。
これを微小電荷\(Δq\)のエネルギー\(ΔW\)の式に代入すると、
\(\displaystyle ΔW=V・Δq=\frac{q}{C}Δq\)
静電エネルギー \(U[J]\)を求めるため、\(ΔW\)を積分すると、
\(\displaystyle U=\int_0^Q ΔW=\int_0^Q \frac{q}{C}dq=\left[ \frac{q^2}{2C} \right]_0^Q=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}CV^2 \)
以上より、
\(\displaystyle U=\frac{1}{2}CV^2\)
が求まりました。
直列接続
直列接続時の合成容量
静電容量\(C_1[F]\)・\(C_2[F]\)の2つのコンデンサを直列接続したときの合成の静電容量\(C[F]\)は、次式の通りです。
\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
直列接続時のコンデンサの合成容量\(C[F]\)の式の証明
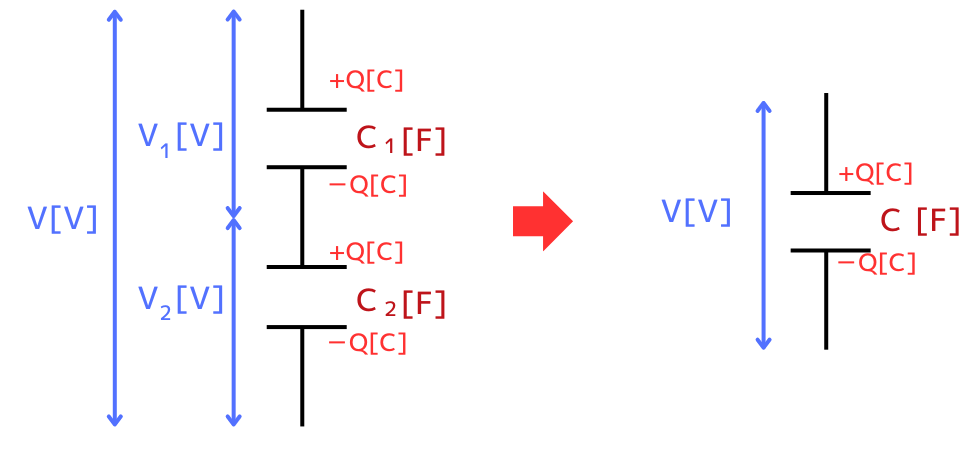
\(C_1[F]\)・\(C_2[F]\)の2つのコンデンサに蓄えられる電荷は、両方とも\(Q[C]\)です。
2つのコンデンサの合成容量を\(C[F]\)とします。\(C[F]\)に蓄えられる電荷も\(Q[C]\)です。
このとき、次の式が成り立ちます。
\(Q=CV=C_1V_1=C_2V_2\) …①
①式から、それぞれの電圧\(V、V_1、V_2\)が求められます。
\(\displaystyle V=\frac{Q}{C}\) …②
\(\displaystyle V_1=\frac{Q}{C_1}\) …③
\(\displaystyle V_2=\frac{Q}{C_2}\) …④
各コンデンサの電圧の関係は
\(V=V_1+V_2\) …⑤
⑤式に②・③・④を代入すると、
\(\displaystyle \frac{Q}{C}=\frac{Q}{C_1}+\frac{Q}{C_2}\)
⇔\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
以上より、直列接続時のコンデンサの合成容量が証明出来ました。
直列接続時の分圧
静電容量\(C_1[F]\)・\(C_2[F]\)の2つのコンデンサを直列接続し、電圧\(V[V]\)の電圧を印加したとき、各コンデンサにかかる電圧\(V_1\)・\(V_2\)は、次式で表されます。
\(\displaystyle V_1=\frac{C_2}{C_1+C_2}V\) 、 \(\displaystyle V_2=\frac{C_1}{C_1+C_2}V\)
直列接続時のコンデンサの分圧の式の証明
直列接続された二つのコンデンサの静電容量を\(C_1[F]\)、\(C_2[F]\)とし、電圧\(V[V]\)を印加したとき、各コンデンサの電圧を\(V_1[V]\)、\(V_2[V]\)とします。
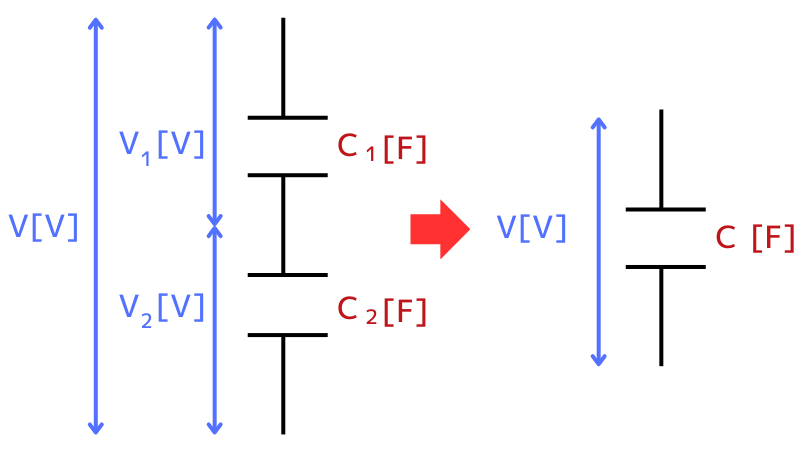
\(C_1\)、\(C_2\)のコンデンサの合成容量\(C\)は、
\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\) ⇔ \(\displaystyle C=\frac{C_1C_2}{C_1+C_2}\) …①
電荷\(Q[C]\)の式に①式を代入して整理します。
\(\displaystyle Q=CV=\frac{C_1C_2}{C_1+C_2}V\) …②
各コンデンサにも同じく電荷\(Q[C]\)が蓄えられるので、
\(Q=C_1V_1=C_2V_2\) …③
③式に②式を代入し、各コンデンサの電圧\(V_1\)、\(V_2\)を求めると、次の通り求まります。
⇔\(\displaystyle V_1=\frac{Q}{C_1}=\frac{C_2}{C_1+C_2}V\)
⇔\(\displaystyle V_2=\frac{Q}{C_2}=\frac{C_1}{C_1+C_2}V\)
以上より、コンデンサの分圧の式が証明できました。
並列接続
並列接続時の静電容量
静電容量\(C_1[F]\)・\(C_2[F]\)の2つのコンデンサを並列接続したときの合成の静電容量\(C[F]\)は、次式の通りです。
\(\displaystyle C=C_1+C_2\)
並列接続時のコンデンサの合成容量\(C[F]\)の式の証明
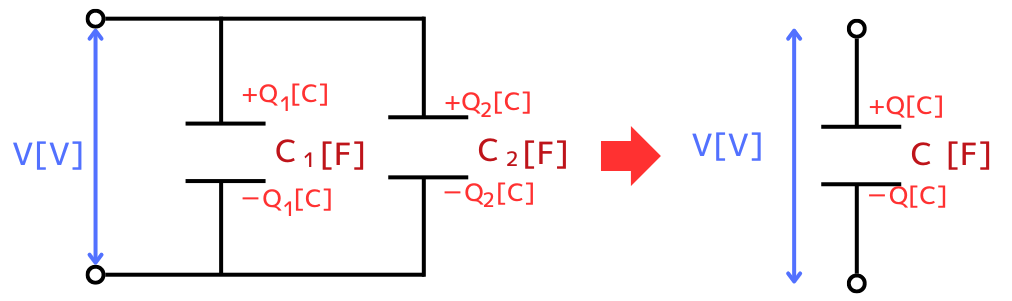
\(C_1[F]\)のコンデンサに蓄えられる電荷は
\(Q_1[C]=C_1V\) …①
\(C_2[F]\)のコンデンサに蓄えられる電荷は
\(Q_2=C_2V[C]\) …②
2つのコンデンサの合成容量を\(C[F]\)とします。\(C[F]\)に蓄えられる電荷は
\(Q=CV[C]\) …③
合成容量の電荷\(Q[C]\)は、\(Q_1[C]\)と\(Q_2[C]\)の電荷の合計なので、
\(Q=Q_1+Q_2\) …④
です。
④式に①・②・③を代入すると、
\(CV=C_1V+C_2V\)
⇔\(C=C_1+C_2\)
以上より、並列接続時のコンデンサの合成容量が証明出来ました。
過去問
難易度 ★★☆☆☆
| 電験三種 平成21年度 問1 (2回目:令和5年度上期 問1) | 電界強度・電束密度・電荷の式の導出 |
| 電験三種 平成21年度 問17 | (a)コンデンサの電界分布の計算 (b)電位の計算 |
難易度 ★★★☆☆
| 電験三種 令和元年度 問2 | 電界強度の計算 |
| 電験三種 令和4年度上期 問1 | 平行平板コンデンサの性質の論説 |
| 電験三種 令和5年度下期 問1 | 平行平板コンデンサの比誘電率の性質の論説 |
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント