ブロック線図の基本
ブロック線図は、システムの入出力関係を示します。
制御工学における重要なシステムの表現方法で、自動制御、電子回路設計、ソフトウェア設計等々、様々な所で使われています。
大規模な電子回路を設計する場合は、ブロック線図を使って回路のシステム全体を設計し、必要な伝達関数を電子回路に落とし込む流れで設計することもあります。
伝達関数の計算
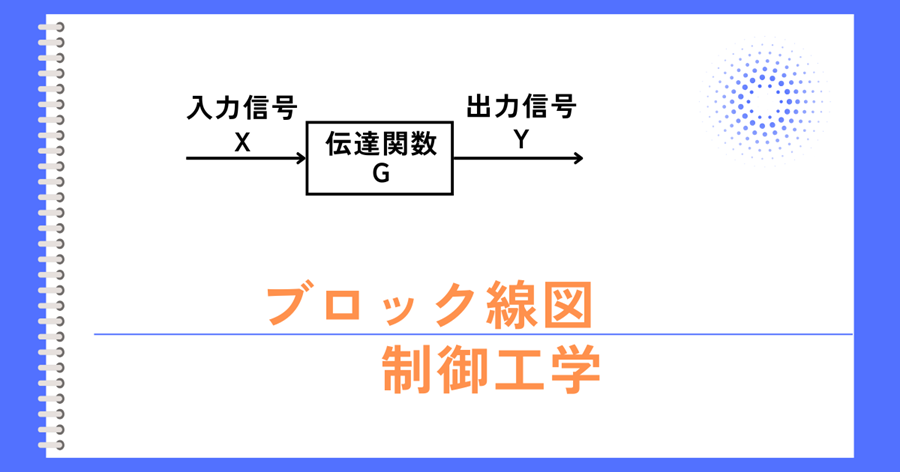
入出力信号と伝達関数
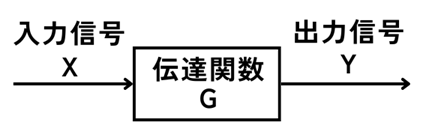
矢印で信号の流れを表し、ブロックでシステムを表します。
左図の例では、伝達関数\(G\)のシステムに\(X\)の信号が入力されると、
\(Y=GX\)
の出力がされます。
加算と減算
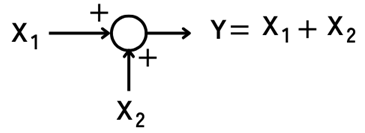
二つの入力信号\(X_1\)・\(X_2\)を加算し、
\(Y=X_1+X_2\)の出力信号を得ます。
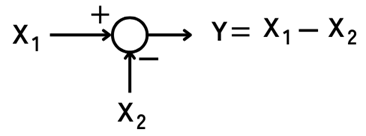
二つの入力信号\(X_1\)・\(X_2\)を減算し、
\(Y=X_1-X_2\)の出力信号を得ます。
分岐
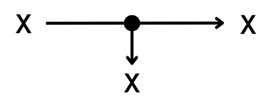
入力信号\(X\)は分岐点で2つの信号にすることができます。
直列接続
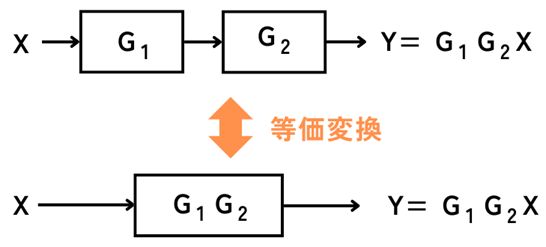
伝達関数\(G_1\)・\(G_2\)の二つのブロックを直列に通った後の出力信号\(Y\)は、
\(Y=G_1G_2X\)
並列接続
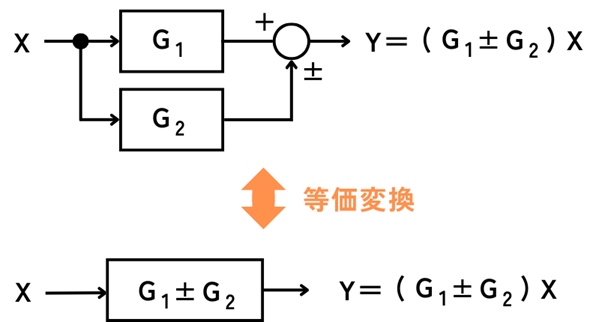
伝達関数\(G_1\)・\(G_2\)の二つのブロックを並列に通った後に加減算した後の出力信号\(Y\)は、
\(Y=(G_1±G_2)X\)
(ネガティブ)フィードバック
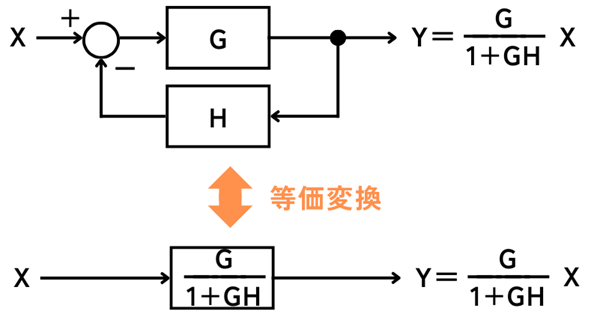
伝達関数\(G\)のブロックの出力信号\(Y\)を、伝達関数\(H\)のブロックを通して入力に戻すことをフィードバックと呼びます。
制御システムにおいて、入力信号から減算するように戻すネガティブフィードバックを使うことが多いです。
この時の出力信号\(Y\)は、
\(\displaystyle Y=\frac{G}{1+GH}X\)
ネガティブフィードバックの導出

①出力信号\(Y\)を伝達関数\(H\)を通し、\(HY\)を入力に戻します。
②入力信号\(X\)から\(HY\)を減算することで算出される信号を偏差\(E\)と呼びます。
\(E=X-HY\)
③\(G\)の入力を偏差\(E\)とした出力がブロックの出力なので、
\(Y=GE=G(X-HY)\)
となります。\(Y\)についてまとめると、
\(\displaystyle Y=\frac{G}{1+GH}X\)
となります。
ブロックの等価変換
加算点の移動
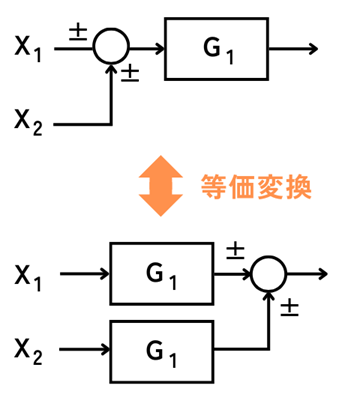
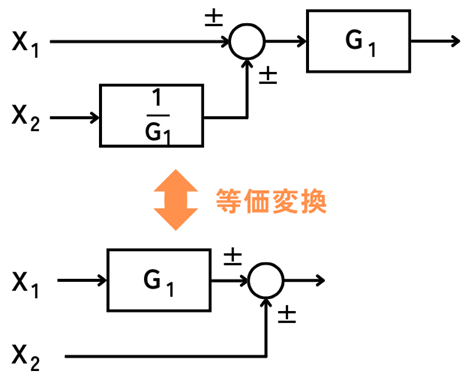
加算点を上図のように、ブロックの前後に移動させることができます。
分岐点の移動
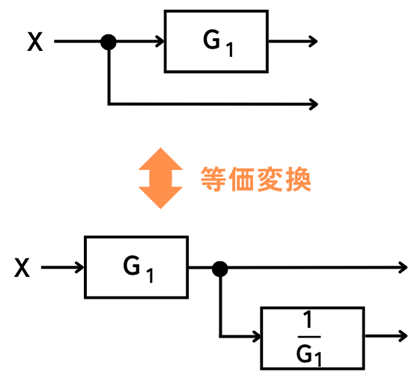
分岐点を左図のように、ブロックの前後に移動させることができます。
ブロック線図と負帰還増幅回路
ネガティブフィードバック回路をブロック線図で表すことができます。
下の図では、非反転増幅回路における、オペアンプのゲイン\(A[dB]\)、フィードバック回路の抵抗値と、伝達関数\(G・H\)がどのように対応するかを示します。
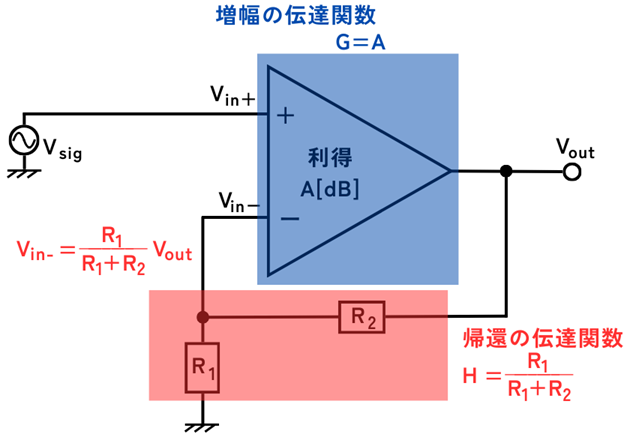
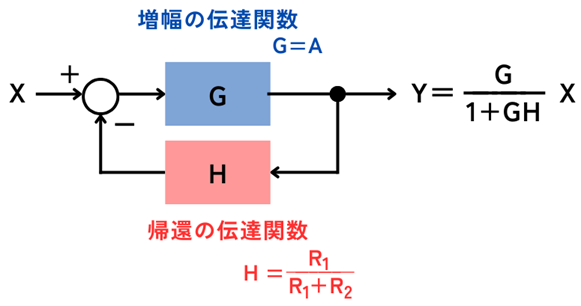
次の1.~3.の流れで、図の回路とブロック線図が対応することについて示していきます。
1.非反転増幅回路の\(V_{out}\)の式を導出
2.ブロック線図の出力\(Y\)の式に回路の値を代入して導出
3.\(V_{out}=Y\)となることを確認する。
1.非反転増幅回路の\(V_{out}\)の式を導出
\(V_{in-}\)は、出力端子\(V_{out}\)から分圧した電圧が供給されるので、
\(\displaystyle V_{in-}=\frac{R_1}{R_1+R_2}V_{out}\) …①
イマジナリーショートから、
\(V_{in-}=V_{in+}\)
⇒ \(V_{in-}=V_{sig}\) …②
②式を①式に代入し、\(V_{out}\)について整理すると、
\(\displaystyle V_{out}=\frac{R_1+R_2}{R_1}V_{sig}\)
⇒ \(\displaystyle V_{out}=(1+\frac{R_2}{R_1})V_{sig}\) …③
2.ブロック線図の出力\(Y\)の式に回路の値を代入して導出
ブロック線図と、非反転増幅回路の対応は、
・増幅の伝達関数\(G=A\)
・帰還の伝達関数\(H=\frac{R_1}{R_1+R_2}\)
です。これらを、ブロック線図の出力に代入します。
\(\displaystyle Y=\frac{G}{1+GH}X=\frac{A}{1+A\frac{R_1}{R_1+R_2}}X\)
理想オペアンプのゲインは\(A=∞\)なので、
\(\displaystyle Y≒\frac{A}{A\frac{R_1}{R_1+R_2}}X\)
と近似できます。整理すると、
\(\displaystyle Y=\frac{R_1+R_2}{R_1}X=(1+\frac{R_2}{R_1})X\) …④
3.\(V_{out}=Y\)となることを確認する。
③式:\(\displaystyle V_{out}=(1+\frac{R_2}{R_1})V_{sig}\)
④式:\(Y=(1+\frac{R_2}{R_1})X\)
入力\(X=V_{sig}\)を代入すると、出力\(Y=V_{out}\)となります。
以上より、図の回路とブロック線図が対応することについて示せました。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント