概要
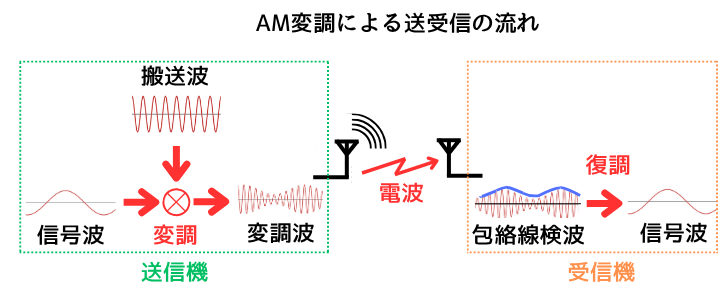
AM変調とは、Amplitude Modulation(振幅変調)の略です。
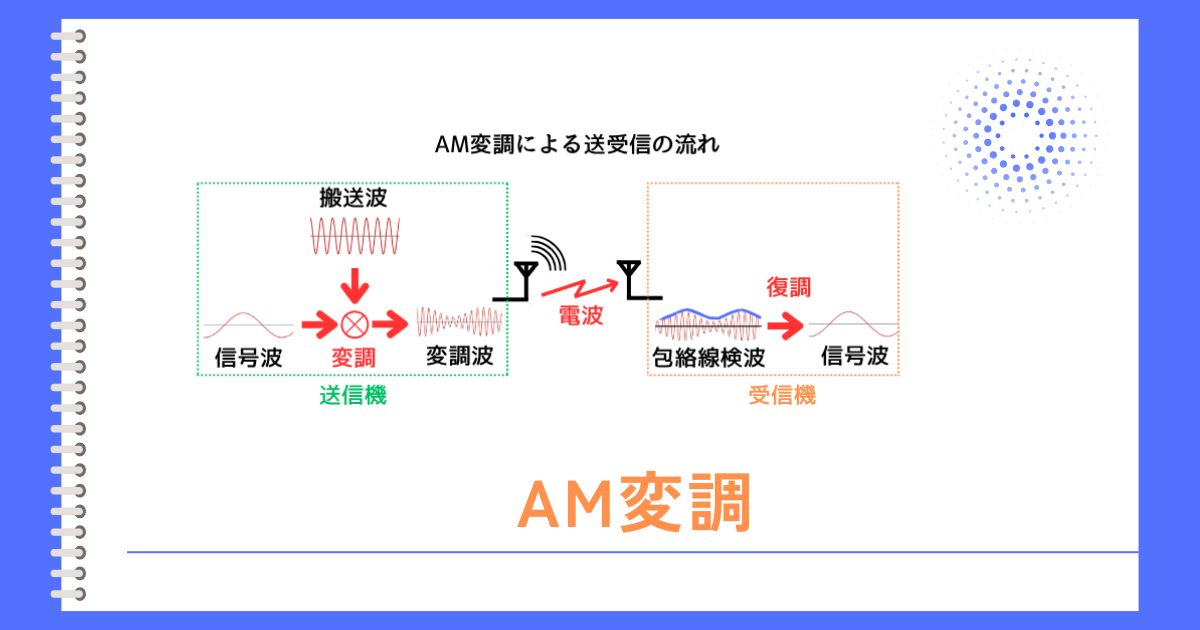
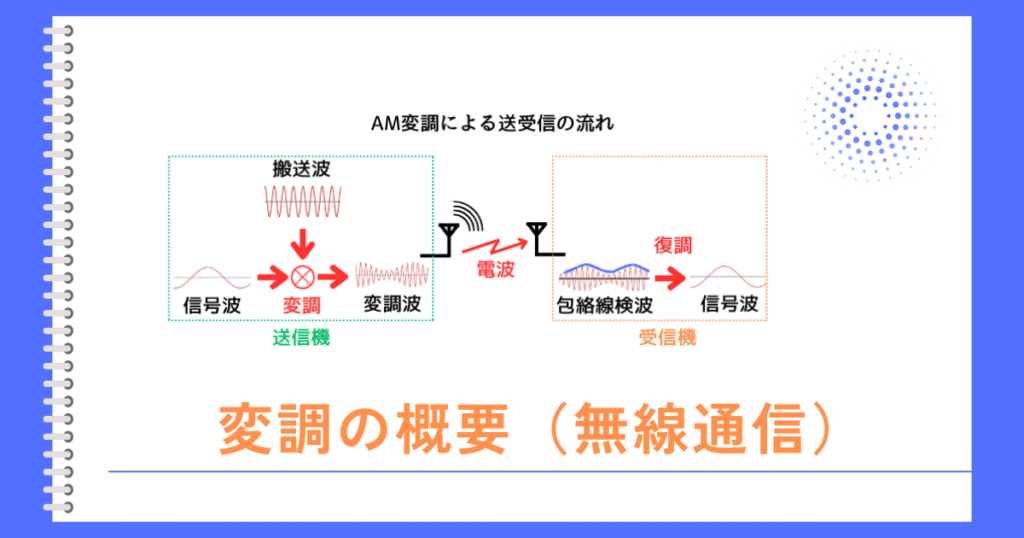
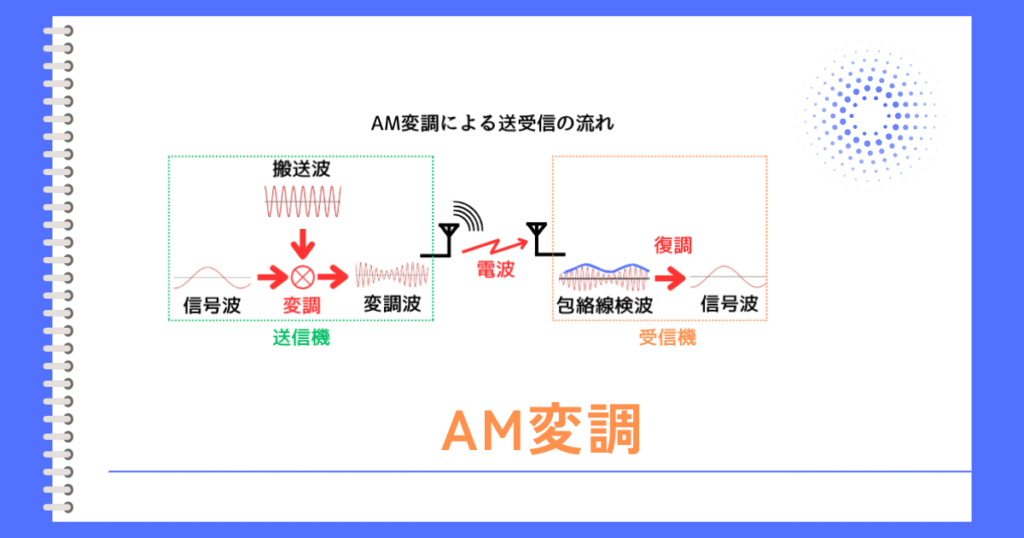
信号波の形に合わせて搬送波の振幅を変化させることで、搬送波に信号波の情報を乗せた変調波にすることが出来ます。
変調波の最大値を取ってつなげることで得られた線を包絡線と呼びます。
受信機では、変調波の中から包絡線を取り出す事で、信号波を得ています。
信号波を取り出すことを復調と呼びますが、検波と呼ぶこともあります。
AM変調は、AMラジオや、航空機無線等で使用されています。
長所
・信号の再現性が高い
・送信機・受信機の構成が簡単
・弱い電波が強い電波にかき消されない
・遠くまで届く
短所
・ノイズの影響を受けやすい
・高い音質が得にくい
変調波
変調度
変調度\(m\)の公式
\(\displaystyle m=\frac{V_s}{V_c}\)
\(V_s\):信号波の振幅、\(V_c\):搬送波の振幅
\(\displaystyle m=\frac{A-B}{A+B}\)
変調度\(m\)は、変調の度合いを示すもので、変調方式や伝送品質に影響を与えます。
信号波の振幅\(V_s\)を搬送波の振幅\(V_c\)で割った値で定義されます。
\(\displaystyle m=\frac{V_s}{V_c}\)
変調度が大きすぎると、歪みやノイズが発生しやすくなり、伝送品質が劣化します。
mが1を超えると過変調になります。過変調になると、受信側で復調した信号が歪むため、\(m<1\)としなければなりません。
変調度が小さすぎると、搬送波の振幅に対して信号の振幅が小さすぎることとなるため、ノイズの影響を受けやすくなり、信号を十分に復調できなくなります。
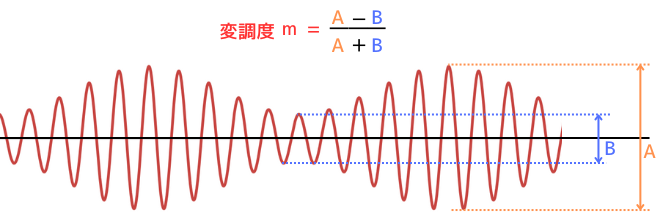
変調波から変調度を読みとるときは、変調波の包絡線のピークを\(A\)、谷を\(B\)としたとき、次式で表されます。
\(\displaystyle m=\frac{A-B}{A+B}\)
\(A\):信号波と搬送波の和が信号の山となるので、\(A=V_c+V_s\)
\(B\):信号波と搬送波の差が信号の底となるので、\(B=V_c-V_s\)
これらを変調度の式に代入すると、
\(\displaystyle m=\frac{A-B}{A+B}=\frac{(V_c+V_s)-(V_c-V_s)}{(V_c+V_s)+(V_c-V_s)}=\frac{2V_s}{2V_c}=\frac{V_s}{V_c}\)
以上より、
\(\displaystyle m=\frac{V_s}{V_c}=\frac{A-B}{A+B}\)
であることがわかりました。
このことから、変調波の最大・最小の振幅が分かれば、変調度が計算できることがわかります。
変調波の瞬時値
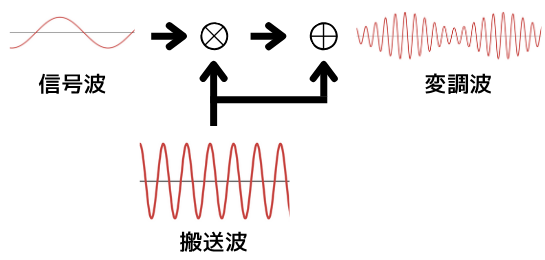
信号波の瞬時値\(v_s\):\(v_s=V_s cosω_st\)
搬送波の瞬時値\(v_c\):\(v_c=V_c sinω_ct\)
変調度を\(m\)とします。
\(\displaystyle m=\frac{V_s}{V_c}\) ⇔ \(V_s=mV_c\)
変調波の瞬時値を\(v_{am}\)とすると、
\(\begin{eqnarray}
v_{am}&=&V_c sinω_ct+v_s sinω_ct \\ \\
&=&V_c sinω_ct+V_s cosω_st・sinω_ct \\ \\
&=&V_c sinω_ct+\frac{V_s}{V_c}V_c cosω_st・sinω_ct \\ \\
&=&V_c sinω_ct+mV_ccosω_st・sinω_ct \\ \\
&=&V_c sinω_ct+\frac{mV_c}{2} \{ sin(ω_c+ω_s)t+sin(ω_c-ω_s)t \} \\ \\
&=&V_c sinω_ct+\frac{mV_c}{2}sin(ω_c+ω_s)t+\frac{mV_c}{2}sin(ω_c-ω_s)t
\end{eqnarray}\)
加法定理
\(sin(A+B)=sinAcosB+cosAsinB\) …①
\(sin(A-B)=sinAcosB-cosAsinB\) …②
①+②より、
\(sin(A-B)+sin(A+B)=2sinAcosB\)
⇔ \(\displaystyle sinAcosB=\frac{sin(A-B)+sin(A+B)}{2}\)
以上より、変調波の瞬時値は、
\(v_{am}=\)\(V_c sinω_ct\)\(+\)\(\displaystyle \frac{mV_c}{2}sin(ω_c+ω_s)t\)\(+\)\(\displaystyle \frac{mV_c}{2}sin(ω_c-ω_s)t\)
と求まりました。
この式から、変調波は次の3つの波で作られていることがわかります。
搬送波:\(V_c sinω_ct\)
上側波帯:\(\displaystyle \frac{mV_c}{2}sin(ω_c+ω_s)t\)
下側波帯:\(\displaystyle \frac{mV_c}{2}sin(ω_c-ω_s)t\)
信号情報は、側波帯(そくはたい)に含まれています。
復調(検波)
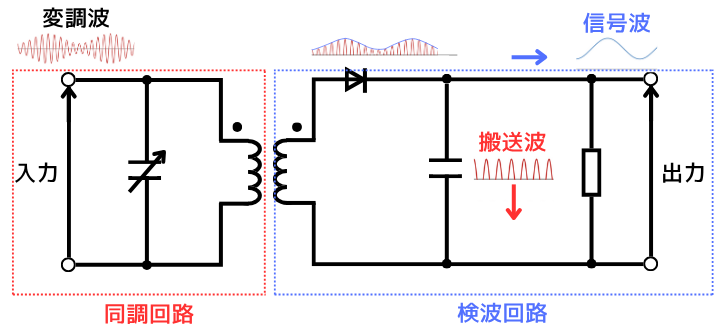
AM受信機の回路は、主に2つの回路で構成されます。
①同調回路
②検波回路
①同調回路
ラジオ局等の送信機から送られる信号は、ラジオ局毎に割り当てられた周波数がそれぞれ異なります。(NHK第一放送594kHz、文化放送1134kHz等々)
アンテナで受信した電波は、異なる周波数の電波を全て受信します。そのため、様々な周波数の信号が複数重なりあった電流信号という形で受信します。
この中から、受信したい放送局からの電波のみを取り出す回路を同調回路と呼びます。
同調回路は、コイルとコンデンサの並列回路で構成されていて、共振周波数の信号だけを取り出すことが出来る回路です。
静電容量を変化させることができるバリコン(バリアブルコンデンサ)を使用しており、静電容量を変化させることで、同調回路の共振周波数も変化させることができます。
②検波回路
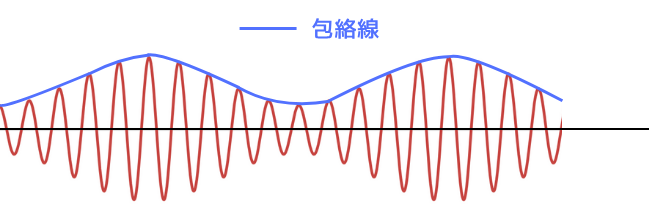
変調波の振幅の頂点を接続すると包絡線が描けます。検波回路は、変調波の中からこの包絡線を取り出すことで信号波を得ることができます。
検波回路は、ダイオードとコンデンサを組合わせた回路です。
コンデンサは低周波に対してはインピーダンスが高く、高周波に対してはインピーダンスが低いです。
そのため、ローパスフィルタとして働きます。
この周波数特性を利用することで、周波数の高い搬送波はコンデンサを通して除去され、周波数の低い信号波だけを出力端子に残すことが出来ます。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント