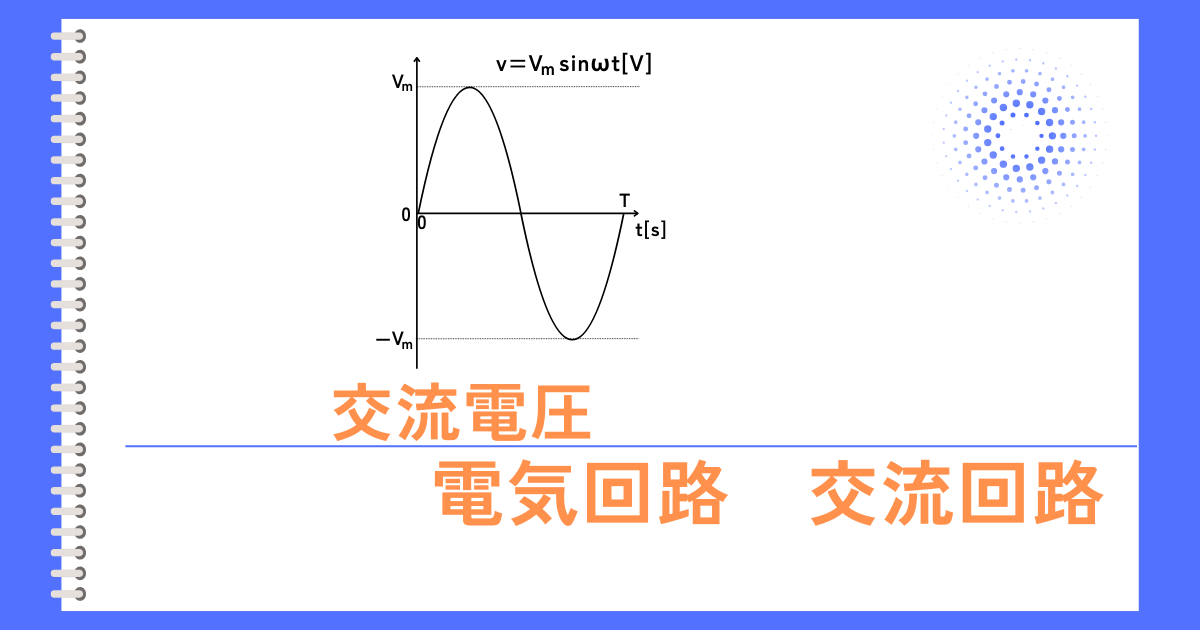
交流電圧
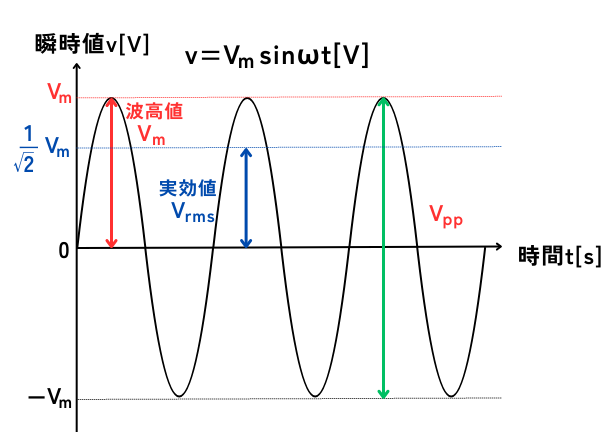
コンセント等の電源から送られてくる交流の電圧\(v\)は、\(v=V_m sinωt\)の数式で表され、時間\(t[s]\)の経過に合わせて常に変化し続けます。
・瞬時値\(v\)
時間tによって変化する、瞬間的な電圧です。
・最大値\(V_m\) (波高値)
基準となる0Vからの、電圧の最大値です。
・\(V_{pp}\) (peak to peak)
正の最大値から負の最大値までの電位差です。
・実効値\(V_{rms}\)
交流電圧を直流電圧に換算した値です。
コンセント等の電源ではAC100V、AC200Vと表現することがありますが、この100V、200Vは実効値を表します。なお、ACは交流(Alternating Current)の意味です。
また、交流電圧計、電流計に表示される値は、実効値が表示されます。
したがって、実効値は実用上で非常に重要な概念です。
電圧実効値\(V_{rms}\)
電圧実効値の意味
電圧の実効値とは、交流を流したときに、直流に換算するとどのくらいになるかを表す電圧です。
ある抵抗\(R[Ω]\)に交流電圧\(v=V_m sinωt[V]\)を加えたときに消費される平均電力\(P_{av}\)とします。
同じ抵抗\(R[Ω]\)に直流電圧\(V_d\)を加えたに消費される電力\(P_d\)とします。
\(P_{av}=P_d\)となるときの直流電圧\(V_d\)が、交流電圧実効値\(V_{rms}\)に相当します。
何故、このように電圧実効値を設定する必要があるのか。
交流回路の電圧、電流は常に大きさも、正・負も変動し続けるため、直流電圧、電流のように簡単に決める事ができません。
単純に交流電圧の平均値を取ると、交流電圧の正・負も周期的に変化し続けるため、0となってしまいます。そのため、単純に平均を取るだけでは大きさを示せません。(電圧の平均値というのは別途あります)
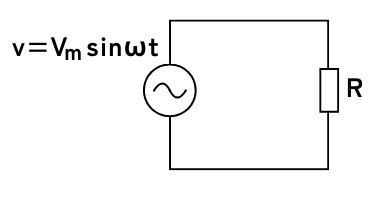
そこで、負荷\(R[Ω]\)に送り込んだ電力が、\(p=\frac{v^2}{R}\)であり、電圧の二乗を取ることを利用します。
電圧の二乗は、交流電圧が負の電圧の瞬間も正の値となります(\((-v)*(-v)=v^2\))。
したがって、消費電力の一周期の平均を取っても0になることはありません。
電圧の大きさを一意に決められる直流電圧に、消費電力を比較する形で換算してしまえば、交流電圧の大きさを決めることが出来ます。
以上のことから、このように電圧実効値が決められます。
電圧実効値\(V_{rms}\)ではなく、電圧の最大値\(V_m\)を電圧として扱うことは出来ないのか?
私が交流を最初に学んだときに疑問に思ったことです。
交流回路は、コンセント電源のように主に正弦波を使うことが多いです。
しかし、交流を直流に変換する回路では半波整流の波形になりますし、方形波、三角波等の様々な波形を扱うこともあります。
そのため、電圧最大値のみで交流電源の電圧を決める事はできません。したがって、最大値ではなく実効値が必要です。
実効値の求め方
実効値の式
\(\displaystyle V_{rms}=\sqrt{\frac{1}{T}\int_0^T v^2dt}\)
実効値の式の証明

交流電圧源に抵抗\(R[Ω]\)が接続されているとします。
電源電圧は、次式の正弦波で表される電源とします。
\(v=V_m sinωt\)
この時の瞬時消費電力\(p\)は、次式で表されます。
\(\displaystyle p=\frac{v^2}{R}=\frac{V_m^2}{R}sin^2ωt=\frac{V_m^2}{R}(1-cos^2 ωt)\)
\(\displaystyle =\frac{V_m^2}{R} \left( 1-\frac{cos2ωt+1}{2}\right)=\frac{V_m^2}{2R}(1-cos2ωt)\)
式変形に使用した三角関数の公式
\(cos^2ωt+sin^2ωt=1\) ⇔ \(sin^2ωt=1-cos^2ωt\)
\(\displaystyle cos^2ωt=\frac{cos2ωt+1}{2}\)
平均消費電力\(P_{av}\)は、1周期積分し、周期Tで割れば求まります。
\(\displaystyle P_{av}=\frac{1}{T}\int_0^T p dt\)
\(\displaystyle =\frac{1}{T}\int_0^T \frac{v^2}{R} dt\) …①
\(\displaystyle =\frac{1}{T}\int_0^T \frac{V_m^2}{2R}(1-cos2ωt)dt\)
\(\displaystyle =\frac{V_m^2}{2R} \frac{1}{T}\int_0^T (1-cos2ωt) dt\)
\(\displaystyle =\frac{V_m^2}{2R} \frac{1}{T}\left[ t-\frac{1}{2ω}sin2ωt \right]_0^T =\frac{V_m^2}{2R} \frac{1}{T}・T\)
\(\displaystyle =\frac{V_m^2}{2R}\) …②
\(\displaystyle =\frac{V_{rms}^2}{R}\) …③
以上より、②=③なので、
\(\displaystyle V_{rms}=\frac{V_m}{\sqrt{2}}\)
このことから、正弦波の電圧の実効値が最大値の\(\frac{1}{\sqrt{2}}\)倍となることが証明出来ました。
また、①=③なので、
\(\displaystyle \frac{1}{T}\int_0^T \frac{v^2}{R} dt =\frac{V_{rms}^2}{R} \)
⇔\(\displaystyle V_{rms}=\sqrt{\frac{1}{T}\int_0^T v^2 dt }\)
以上より、電圧の実効値の式を証明することができました。
\(P_{av}\)を求めるために、\(p\)を1周期積分し、周期Tで割る理由の補足
仮に、1周期\(T=10s\)としたとき、瞬時消費電力\(p\)を1周期分積分すると、10秒間で消費される電力量が求まります。
消費電力は、1秒間で消費される電力なので、周期\(T=10s\)で割ることで、平均消費電力を求めることが出来ます。
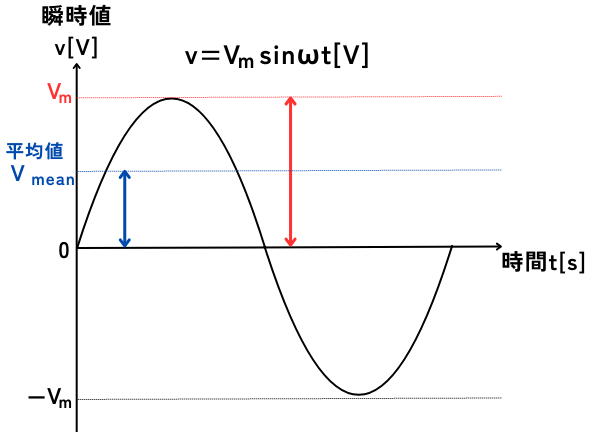
平均値\(V_{ave}\)
交流電圧の平均値は、1周期分の積分を行った後、周期T秒で割ることで求めることができます。
しかし、正弦波\(v=V_m sinωt\)はマイナスの値も取るため、1周期を単純に積分すると、値は0となります。
そこで、電圧の大きさ\(|v|\)の積分を取ることで、平均値を求めることができます。
平均値の式
\(\displaystyle V_{ave}=\frac{1}{T}\int_0^T |v|dt\)
正弦波 \(v=V_m sinωt\) の平均値の導出
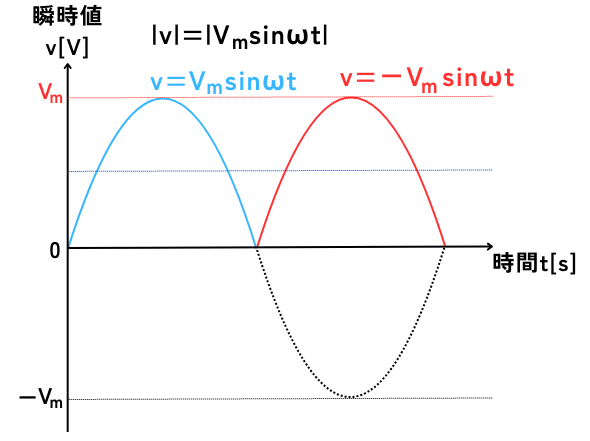
\(\displaystyle V_{ave}=\frac{1}{T}\int_0^T |v|dt\)
⇔\(\displaystyle V_{ave}=\frac{1}{T}\int_0^T |V_m sinωt| dt\)
\(0から\frac{T}{2}\)の期間は、正弦波はプラスですが、\(\frac{T}{2}からT\)の期間は正弦波はマイナスになるので、次のように式を分けます。
⇔\(\displaystyle V_{ave}=\frac{1}{T} \left( \int_0^{\frac{T}{2}} V_m sinωt dt+\int_{\frac{T}{2}}^T -V_m sinωt dt \right) \)
⇔\(\displaystyle V_{ave}=\frac{1}{T} \left( \frac{V_m}{ω} [-cosωt]_0^{\frac{T}{2}}-\frac{V_m}{ω} [-cosωt]_{\frac{T}{2}}^T \right) \)
⇔\(\displaystyle V_{ave}=\frac{V_m}{ωT} \left( -cos\frac{ωT}{2}+cos0+cosωT-cos\frac{ωT}{2} \right) \)
⇔\(\displaystyle V_{ave}=\frac{V_m}{ωT} \left( -(-1)+1+1-(-1) \right)=\frac{4V_m}{ωT} \)
⇔\(\displaystyle V_{ave}=\frac{4V_m}{2πfT}=\frac{2V_m}{π}=0.637V_m \)
周波数\(f\)、周期\(T\)としたとき、
\(f=\frac{1}{T}\)なので、
\(fT=\frac{1}{T}T=1\)
\(ωT=2πfT=2π\frac{1}{T}T=2π\)
\(cosωT=cos2π=cos0=1\)
\(\frac{ωT}{2}=πfT=π\frac{1}{T}T=π\)
\(cos \frac{ωT}{2}=cosπ=-1\)
波形率
波形率は、平均値に対する実効値の比で、次式で表されます。
\(\displaystyle 波形率=\frac{実効値V_{rms}}{平均値V_{ave}}\)
波形率の意味は、交流波形が、どれだけ直流波形(平均値=実効値)に近いかを示します。
・直流の波形率 :1
・正弦波の波形率:1.11
正弦波の波形率
\(V_{rms}=\frac{1}{\sqrt{2}}V_m\)
\(V_{ave}=\frac{2}{π}V_m\)
\(\displaystyle 波形率=\frac{V_{rms}}{V_{ave}}=\frac{\frac{1}{\sqrt{2}}V_m}{\frac{2}{π}V_m}=\frac{π}{2\sqrt{2}}=1.11\)
波高率
波高率とは、交流波形の実効値に対するピーク値の比率であり、次式で表されます。
\(\displaystyle 波高率=\frac{波高値V_m}{実効値V_{rms}}\)
波高率は交流電源の電源品質のパラメータとして使われ、波高率が高くなると力率が悪い状態を示します。
波高率が1.41に近いと良好な電源ですが、波高率が上昇すると、次のような悪影響があります。
・力率が悪化して電力損失が増加する
・瞬間的な高い値を示す
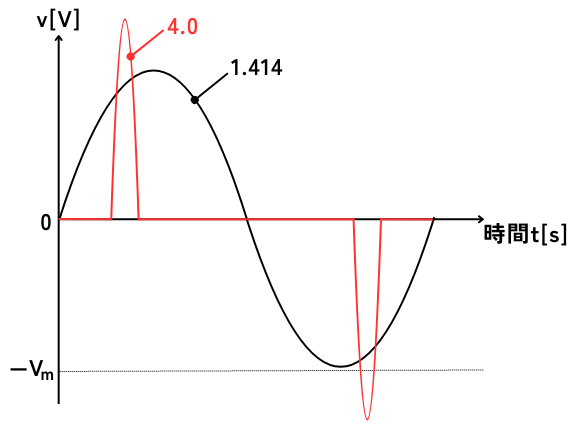
波高率による波形を図示すると、左図のようになります。
正弦波の波高率
波高値:\(V_m\)
実効値:\(V_{rms}=\frac{1}{\sqrt{2}}V_m\)
\(\displaystyle 波高率=\frac{V_m}{V_{rms}}=\frac{V_m}{\frac{1}{\sqrt{2}}V_m}=\sqrt{2}=1.414\)
周期T
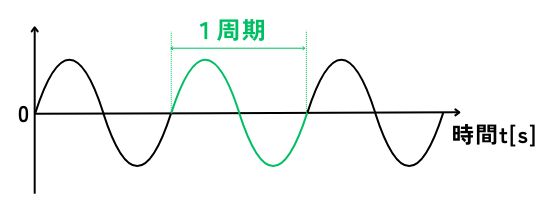
波が上下に1回振動するのにかかる時間です。
上下に1回振動するのに2秒かかったとすると、
周期\(T=2s\)です。
周波数\(f[Hz]\)との関係は、次式で表されます。
\(\displaystyle T=\frac{1}{f}\)
周波数f
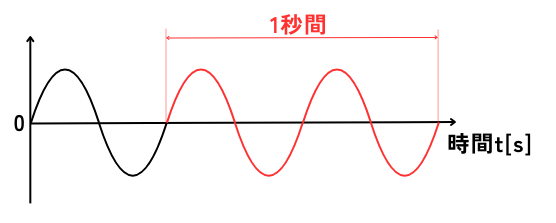
1秒間に波が上下に振動する回数が周波数です。
左図の例だと、1秒間に2回上下に振動しているので、
周波数\(f=2Hz\)です。
周期\(T[s]\)との関係は、次式で表されます。
\(\displaystyle f=\frac{1}{T}\)
角周波数ω
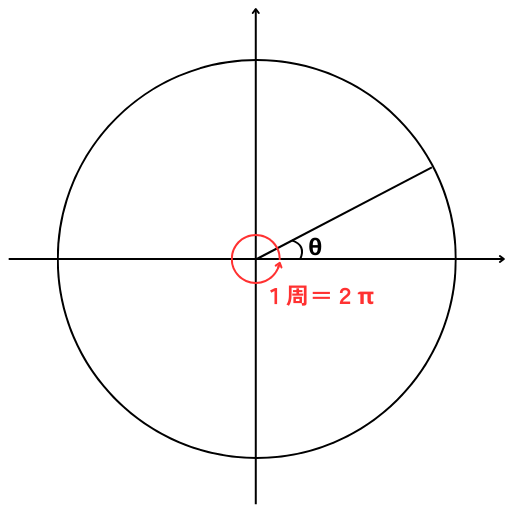
角周波数は、1秒間に何rad変化したかを表すものです。
交流波形が1周期すると、円を1周描きますので、位相角の変化は\(2π[rad]\)です。
1秒間に1周期したときの角周波数の変化は、\(ω=2π[rad/s]\)となります。この時の周波数は\(f=1Hz\)です。
したがって、角周波数ωと周波数fの関係は、
\(ω=2πf\)です。
関連記事(交流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント