難易度
RL回路の過渡現象に関する問題です。
過渡現象の計算は、比較的難しい（面倒くさい）部類の単元ですが、この問題はその中では初歩の内容です。
この問題を押さえられるか否かが合否を分けると思います。
問題
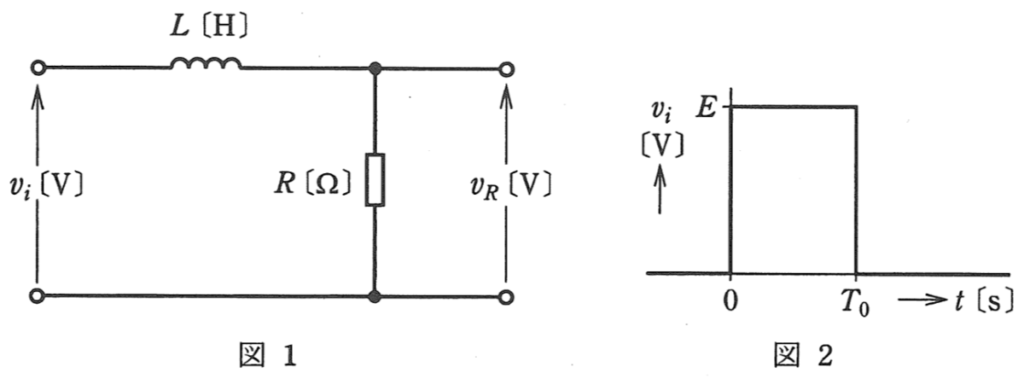
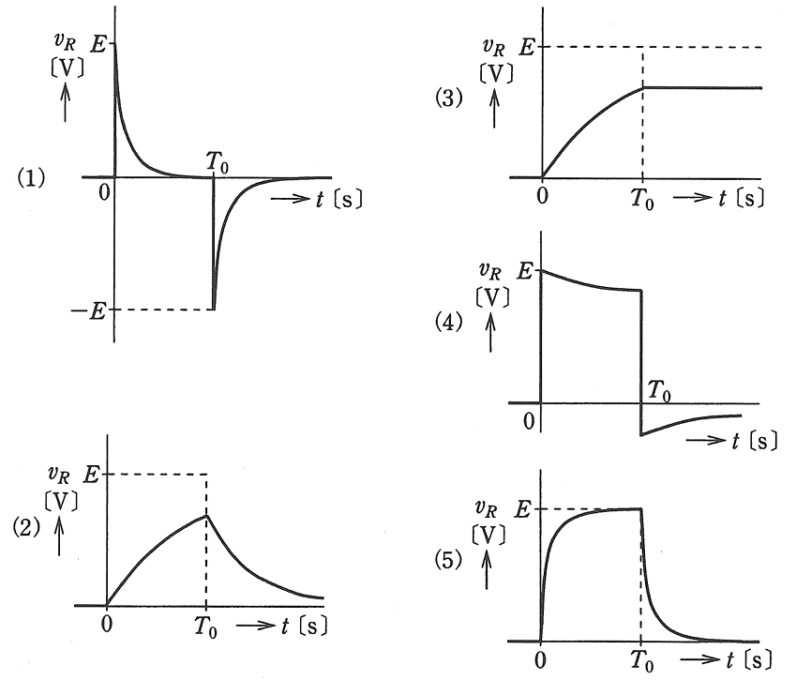
図１のようなインダクタンス\(L[H]\)のコイルと\(R[Ω]\)の抵抗からなる直列回路に、図２のような振幅\(E[V]\)、パルス幅\(T_s[s]\)の方形波電圧\(v_i[V]\)を加えた。このときの抵抗\(R[Ω]\)の端子間電圧\(v_R[V]\)の波形を示す図として、正しいのは次のうちどれか。
ただし、図１の回路の時定数\(\displaystyle \frac{L}{R}[s]\)は\(T_s[s]\)より十分小さく\(\displaystyle \frac{L}{R} \ll T_s\)、方形波電圧\(v_i[V]\)を発生する電源の内部インピーダンスは\(0[Ω]\)とし、コイルに流れる初期電流は\(0[A]\)とする。
回答
答え
(５)
要点整理
解き方は４種類あります。
本ページでは、初等解析法と、初期状態・定常状態から解く方法の２つの回答を紹介します。
1.初等解析法で解く
⇒ 電験三種の問題に一番適した解法です。
2.初期状態・定常状態から解く
⇒ 電験三種の過渡解析だと使える事が多いです。
3.ラプラス変換で解く
⇒ 様々な回路に応用できるが、覚える事が多いです。
電験二種ではマスター必須なので、二種受験時に学ぶと良いでしょう。
4.微分方程式を数学的に解く
⇒ 本質的な解法ではあるけれども、手間が掛かり過ぎるので使えません。
初等解析法での回答
初等解析法で解く方法の流れは以下の流れです。
①回路図から微分方程式を作る
②過渡状態の\(v_R\)の電圧：\(v_{Rt}\)を解析する
③定常状態の\(v_R\)の電圧：\(v_{Rs}\)を解析する
④\(v_R=v_{Rt}+v_{Rs}\)とすることで、抵抗Rにかかる電圧の式を組み立てる
⑤初期条件\(t=0[s]\)から、\(v_R\)の式中の未定だった係数を導き出す
⇒完了
文字に手順を起こすと少々手順が多いように見えますが、実際多いです。
しかし、ラプラス変換で解く方法や、微分方程式から数学的に解く方法よりは圧倒的に楽で早いです。
回路中に流れる電流を\(i\)とします。この時、
抵抗の両端に発生する電圧\(v_R\)は、オームの法則から、\(v_R(t)=Ri(t)\) …(1)
リアクトルの両端に発生する電圧\(v_L\)は、\(\displaystyle v_L(t)=L\frac{di(t)}{dt}\) …(2)
電流が変動している時にしか電圧が発生しないことがわかります。
(1)式を変形すると、\(\displaystyle i(t)=\frac{v_R(t)}{R}\)…(3)
(3)式を(2)式に変形すると、\(\displaystyle v_L(t)=\frac{L}{R}・\frac{dv_R(t)}{dt}\)…(4)
図１の回路に(4)を代入して微分方程式を作ると
\(\displaystyle v_i(t)=v_L(t)+v_R(t)=\frac{L}{R}・\frac{dv_R(t)}{dt}+v_R(t)\) …(5)
となります。この(5)式を使って、過渡状態、定常状態の２つの状態について解析していきます。
・過渡状態
過渡状態の時の\(v_R(t)\)は、\(v_{Rt}\)とします。
このとき、(5)式中の変数に下記(6)(7)(8)をあてはめます。
\(v_i(t)=0\) …(6)
\(v_{Rt}=ke^{-st}\) …(7)
(7)式を微分すると、
\(\displaystyle \frac{dv_{Rt}}{dt}=-ske^{-st}\) …(8)
(5)式は、
\(\displaystyle \frac{L}{R}(-ske^{-st})+ke^{-st}=(1-\frac{L}{R}s)ke^{-st}=0\)
となり、\(\displaystyle s=\frac{R}{L}\) …(9)
(9)式を(7)式に代入すると、過渡状態の\(v_{Rt}\)は、
\(\displaystyle v_{Rt}=ke^{-\frac{R}{L}t}\) …(10)
・定常状態
定常状態になると、電流・電圧の変化は無くなるので、(5)式中の微分項は0となります。
定常状態の\(v_R(t)\)は、\(v_{Rs}\)としますと、
\(\displaystyle \frac{dv_{Rs}}{dt}=0\) …(11)
(11)を(5)式に代入すると、
\(\displaystyle v_{Rs}=v_i\) …(12)
・まとめ（\(v_R(t)=\)過渡状態\(v_{Rt}\)+定常状態\(v_{Rs}\)）
過渡状態\(v_{Rt}\)、定常状態\(v_{Rs}\)を足し合わせることで、\(v_R(t)\)の式を導き出せます。
(10)式と、(12)式から、
\(v_R(t)=v_{Rt}+v_{Rs}=ke^{-\frac{R}{L}t}+v_i\) …(13)
係数kを初期条件から求めます。
\(t=0\) …(14)
のとき、リアクトルLは開放状態として扱うので、
\(v_R(0)=0\) …(15)
また、この時入力電圧\(v_i\)は、\(E\)になるので、
\(v_i=E\) …(16)
(14)・(15)・(16)式を(13)式に代入すると、
\(0=ke^0+E\)
⇔\(k=-E\) …(17)
(13)式に(16)・(17)式を代入すると、
\(v_R=(1-e^{-\frac{R}{L}t})E\) …(18)
以上で、\(t=0～T_0\)の間の過渡解析が終わりました。
・まとめ２（\(v_R(t)=\)過渡状態\(v_{Rt}\)+定常状態\(v_{Rs}\)）
次に、\(t=T_0\)で、\(v_i(T_0)=0\)となった時を解析します。
このときの初期条件は、
\(v_R(T_0)=E\) …(18)
\(v_i(T_0)=0\) …(19)
(18)・(19)式を、(13)式に代入します。
\(v_R(T_0)=E=ke^{-\frac{R}{L}(t-T_0)}+0\) …(20)
このとき、\(T_0\)が過渡状態の開始点になるので、
(20)式中の時間の変数が\((t-T_0)\)となっている点に注意してください。
(20)式に\(t=T_0\)を代入して解くと、
\(k=E\) …(21)
以上より、(20)式に(21)式を代入すると、
\(v_R(t)=Ee^{-\frac{R}{L}(t-T_0)}\) …(22)
と、求まります。
これをグラフに書くと、(5)が答えとなります。
初期状態・定常状態から解く
RC回路、RL回路過渡解析を何回かやっていて、どのような波形を描くか何となく推察できるようになっている場合、この方法だと時間が掛からずに解けるためお勧めです。
下記①～④の４つの状態について、解析します。
①\(t=0\)で、\(v_i=E\)になったときの初期状態
リアクトル\(L\)は、開放状態となるので、電流は流れません。
そのため、\(v_R(0)=0\)とわかります。
②\(t≦T_0\)の定常状態
リアクトル\(L\)は、短絡状態となるので、全ての入力電圧が抵抗にかかります。
そのため、\(v_R=v_i=E\)とわかります。
③\(t=T_0\)の初期状態
リアクトル\(L\)は、開放状態となるので、電流は流れません。
そのため、直前の②の状態と同じで\(v_R(T_0)=E\)とわかります。
④\(t=\infty\)の定常状態
リアクトル\(L\)は、短絡状態となるので、全ての入力電圧が抵抗にかかります。
そのため、\(v_R=v_i=0\)とわかります。
４つの状態がわかったので、各状態の間を補間します。
①～②間を補間します。問題から、時定数\(τ=\frac{L}{R}[s]\)がわかっていますので、
τ秒経過後、最終値E[V]の63%の電圧まで来ます。つまり、\(v_R=0.63E[V]\)
2τ秒経過後、最終値E[V]の86%の電圧まで来ます。つまり、\(v_R=0.86E[V]\)
3τ秒経過後、最終値E[V]の95%の電圧まで来ます。つまり、\(v_R=0.95E[V]\)
②～③間は、両方\(v_R(T_0)=E\)です。
③～④間は、
τ秒経過後、最終値0[V]の63%の電圧まで来ます。つまり、\(v_R=(1-0.63)E=0.37E[V]\)
2τ秒経過後、最終値0[V]の86%の電圧まで来ます。つまり、\(v_R=(1-0.86)E=0.14E[V]\)
3τ秒経過後、最終値0[V]の95%の電圧まで来ます。つまり、\(v_R=(1-0.95)E=0.05E[V]\)
グラフにすると、下図のようになります。
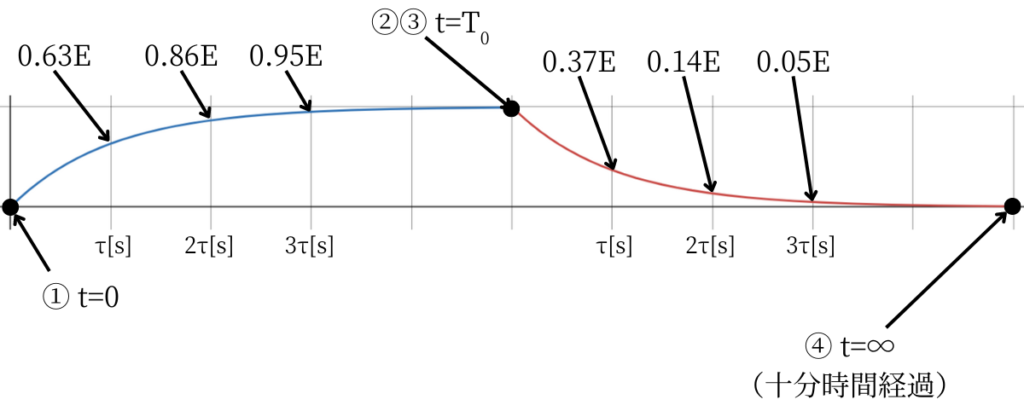
以上より、答えは(5)です。
時定数τに応じた数値は、覚える必要はありませんが、τ秒経過したら6割、2τ経過したら8割、3τ秒経過したら9割程度に覚えておくと楽な場面はあります。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問１０
参考書
本ブログの管理人は、電験３種過去問マスタを使って３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント