概要
演算増幅器(オペアンプ)について問う問題と、オペアンプを使用した負帰還増幅回路について問う論説問題です。
基礎レベルの内容なので、確実に回答したい問題です。
キーワード
演算増幅器、オペアンプ、負帰還増幅回路、正相増幅回路、逆相増幅回路、比較器、ボルテージホロワ
問題
演算増幅器及びそれを用いた回路に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
(1)演算増幅器には電源が必要である。
(2)演算増幅器の入力インピーダンスは、非常に大きい。
(3)演算増幅器は比較器として用いられることがある。
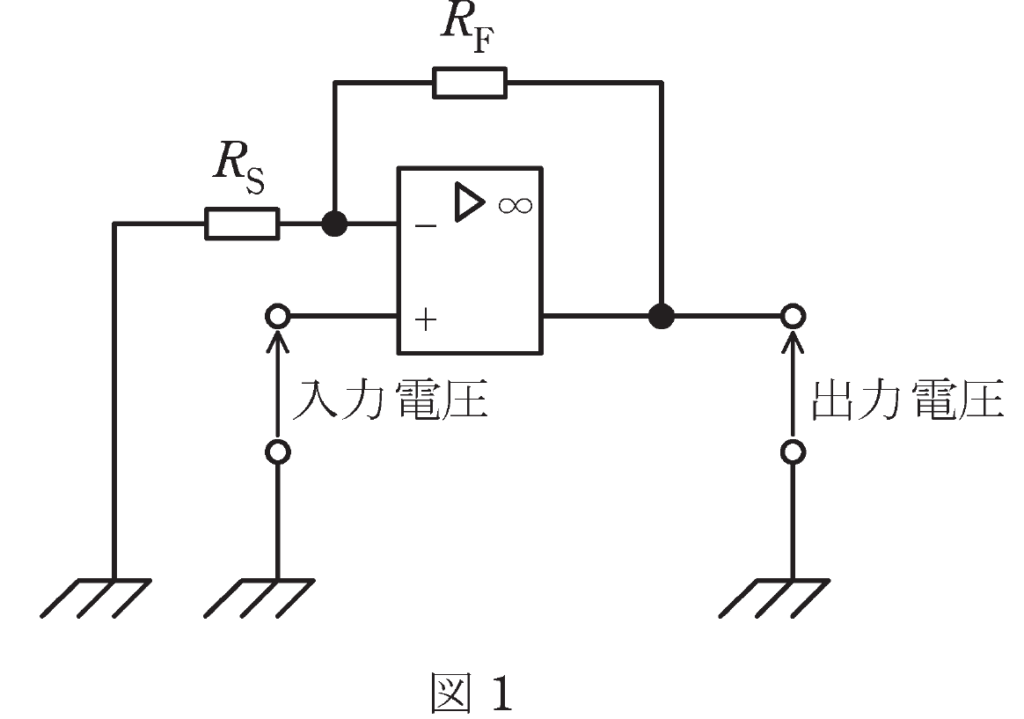
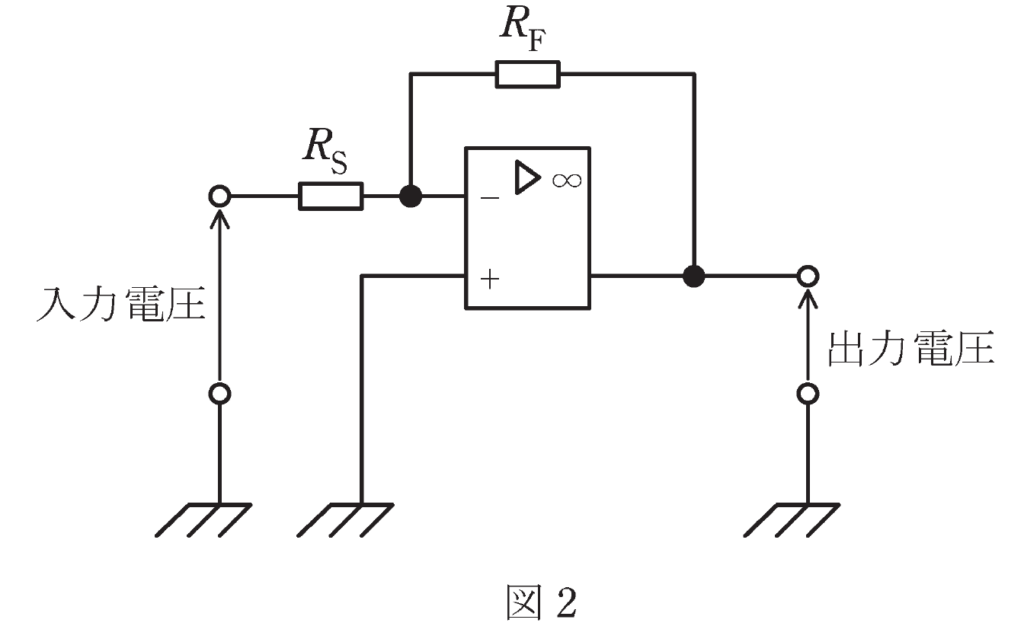
(4)図1の回路は正相増幅回路、図2の回路は逆相増幅回路である。
(5)図1の回路は、抵抗\(R_s\)を\(0Ω\)に(短絡)し、抵抗\(R_F\)を\(∞Ω\)に(開放)すると、ボルテージホロワである。
答え
(5)
解説テキスト リンク
回答解説
(1)演算増幅器には電源が必要である。
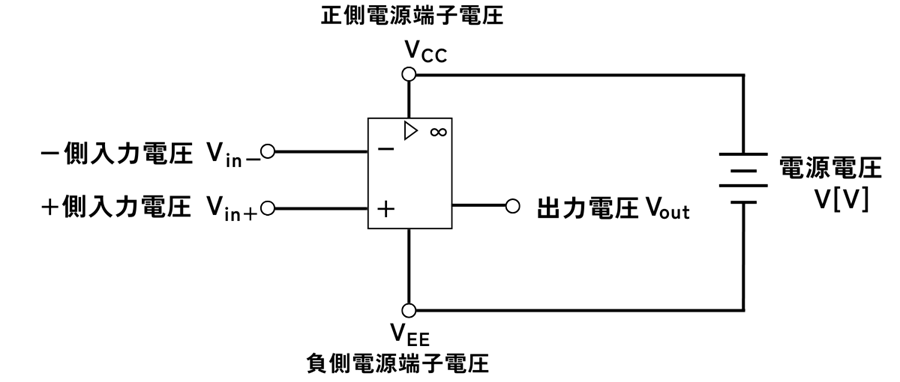
演算増幅器には電源が必要です。
正側電源と、負側電源に直流電圧源を接続することで、演算増幅器は入力信号を増幅することができるようになります。
(2)演算増幅器の入力インピーダンスは、非常に大きい。
演算増幅器の理想的な特性は、下表のとおりです。入力インピーダンスの理想特性は\(∞[Ω]\)であるため、入力インピーダンスは、非常に大きいことが求められます。
| 利得(ゲイン) | \(∞[dB]\) |
| 遮断周波数(カットオフ周波数) | \(∞[Hz]\) |
| 入力インピーダンス | \(∞[Ω]\) |
| 出力インピーダンス | \(0[Ω]\) |
(3)演算増幅器は比較器として用いられることがある。
演算増幅器の二つの入力\(V_{in+}・V_{in-}\)の電位差が電圧増幅率\(A_v\)[倍]増幅されて出力\(V_{out}\)されます。
\(V_{out}=A_v(V_{in+}-V_{in-})\)
演算増幅器の理想的な電圧増幅率は\(A_v=∞\)です。そのため、
\(V_{in+}>V_{in-}\)のときの出力電圧は、正側電源端子電圧\(V_{CC}\)
\(V_{in+}<V_{in-}\)のときの出力電圧は、負側電源端子電圧\(V_{EE}\)
となります。
したがって、演算増幅器は、比較器として用いることができます。
(4)図1の回路は正相増幅回路、図2の回路は逆相増幅回路である。
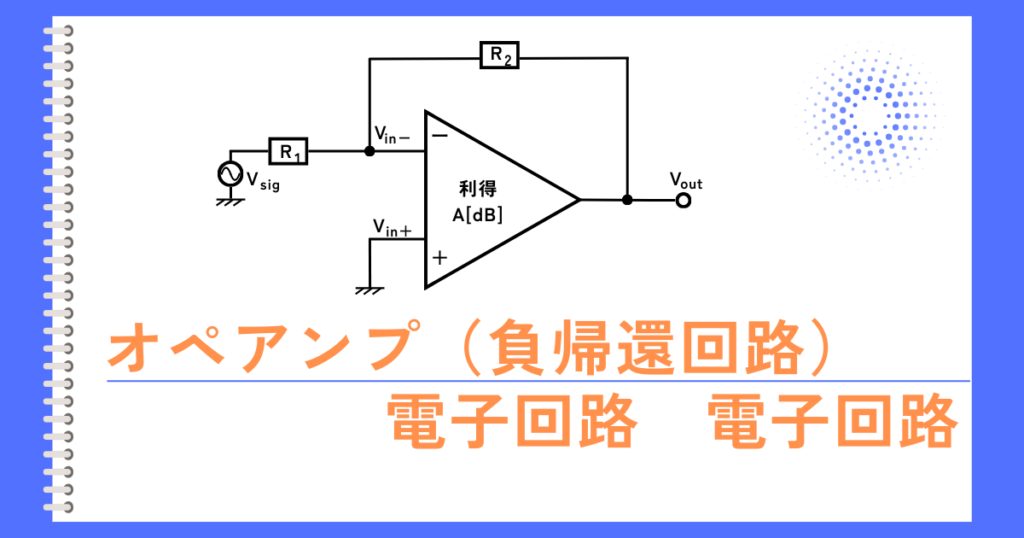
図1の回路について解析します。
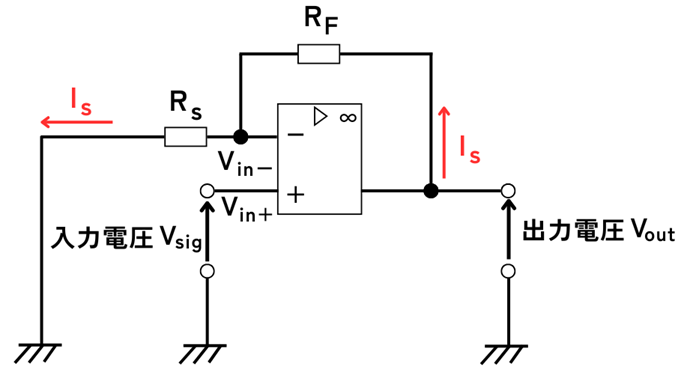
演算増幅器の\(-\)側の入力端子の電圧\(V_{in-}\)は、出力端子\(V_{out}\)から分圧した電圧が供給されますので、
\(\displaystyle V_{in−}=\frac{R_s}{R_s+R_F}V_{out}\) …①
イマジナリーショートの考え方から、\(+\)側の入力端子の電圧\(V_{in+}\)と、\(-\)側の入力端子の電圧\(V_{in-}\)は同じ電圧となります。
\(V_{in+}=V_{in-}\) …②
入力電圧\(V_{sig}\)がそのまま\(+\)側の入力端子に入力されるので、
\(V_{in+}=V_{sig}\) …③
①・②・③式から、出力電圧\(V_{out}\)が求まります。
\(\displaystyle V_{out}=\frac{R_s+R_F}{R_s}V_{sig}=\left( 1+\frac{R_F}{R_s}\right) V_{sig}\)
以上より、入力電圧\(V_{sig}\)と出力電圧\(V_{out}\)の符号は+であるため、2つの抵抗\(R_F\)、\(R_s\)で増幅率が決められる正相増幅回路です。
図2の回路について解析します。
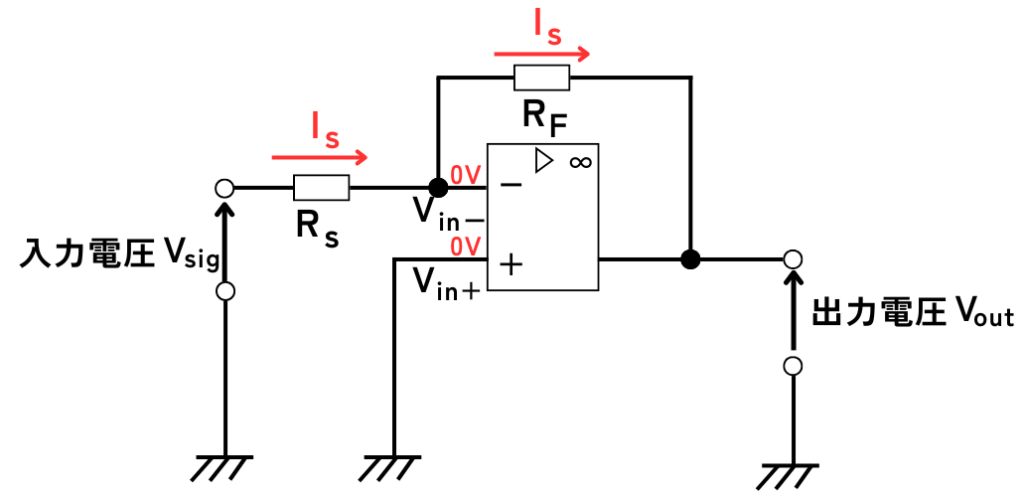
演算増幅器の\(+\)側の入力端子の電圧\(V_{in+}\)は、接地しているため0Vです。
イマジナリーショートにより、
\(V_{in−}=V_{in+}=0V\)です。
入力電圧信号を\(V_{sig}\)とします。\(V_{sig}\)から\(V_{in−}\)に抵抗\(R_s\)を通って流れる電流\(i_s\)は、
\(\displaystyle i_s=\frac{V_{sig}}{R_s}\) …①
オペアンプの入力インピーダンスの理想特性は\(Z_{in}=∞\)なので、\(V_{in−}\)からオペアンプ内に電流は流れません。
したがって、\(V_{sig}\)から流れ込んできた\(i_s\)は、抵抗\(R_F\)を流れて全て出力端子\(V_{out}\)に流れます。
抵抗\(R_F\)の両端の端子間電圧は、\(0V-V_{out}\)なので、
\(\displaystyle i_s=\frac{0−V_{out}}{R_F}=\frac{−V_{out}}{R_F}\) …②
①=②式から、
\(\displaystyle \frac{V_{sig}}{R_s}=\frac{−V_{out}}{R_F}\)
⇔ \(\displaystyle V_{out}=-\frac{R_F}{R_s}V_{sig}\)
以上より、入力電圧信号\(V_{sig}\)と出力電圧\(V_{out}\)の符号は-であるため、2つの抵抗\(R_F\)、\(R_s\)で増幅率が決められる逆相増幅回路です。
(5)図1の回路は、抵抗\(R_s\)を\(0Ω\)に(短絡)し、抵抗\(R_F\)を\(∞Ω\)に(開放)すると、ボルテージホロワである。
選択肢の文章のとおり、\(R_s=0Ω\)、\(R_F=∞Ω\)とすると、下図のように、ただのオープンループ接続となりますので、ボルテージホロワにはなりません。
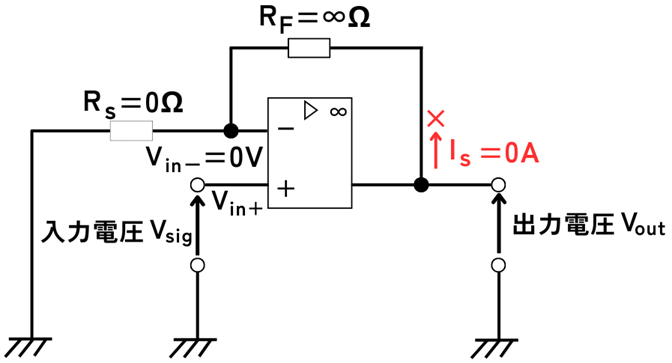
➡
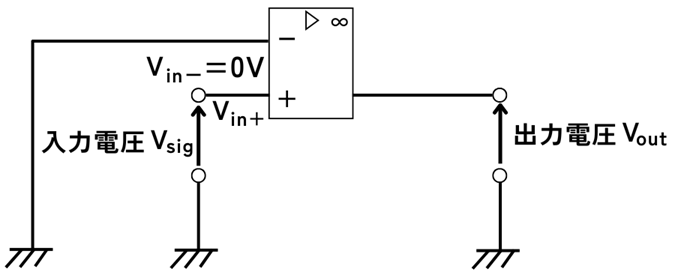
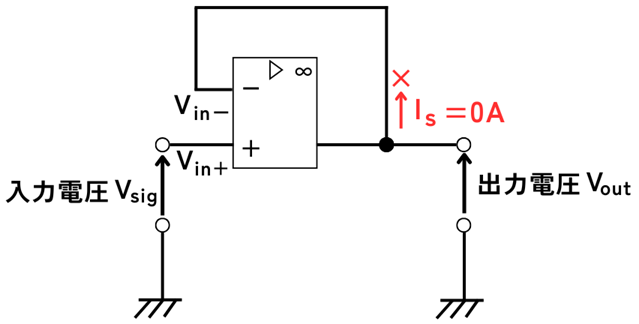
ボルテージホロワ回路を作りたいときは、\(R_s=∞Ω\)、\(R_F=0Ω\)とすることで作ることが出来ます。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和2年度 第三種電気主任技術者試験 理論科目A問題問13
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント