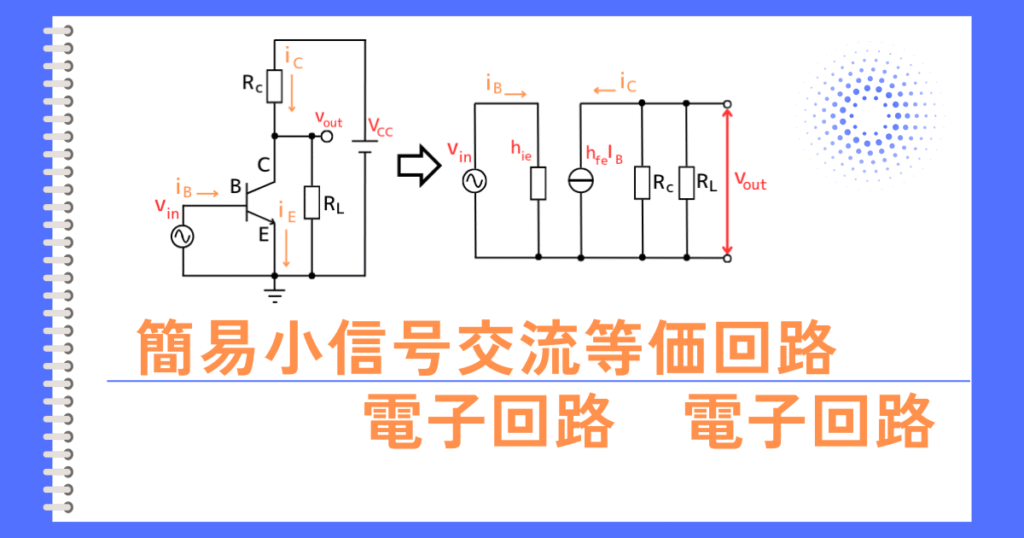
フィードバック(帰還)とは
フィードバック(帰還)とは、オペアンプの出力信号の一部を、入力信号に戻し、入力と出力を比較することで、必要な出力になるように調整・制御する方法です。
フィードバックには、ポジティブフィードバック(正帰還)と、ネガティブフィードバック(負帰還)の2種類のフィードバックがあります。
本ページでは、ポジティブフィードバックについて解説します。
ポジティブフィードバック(正帰還)
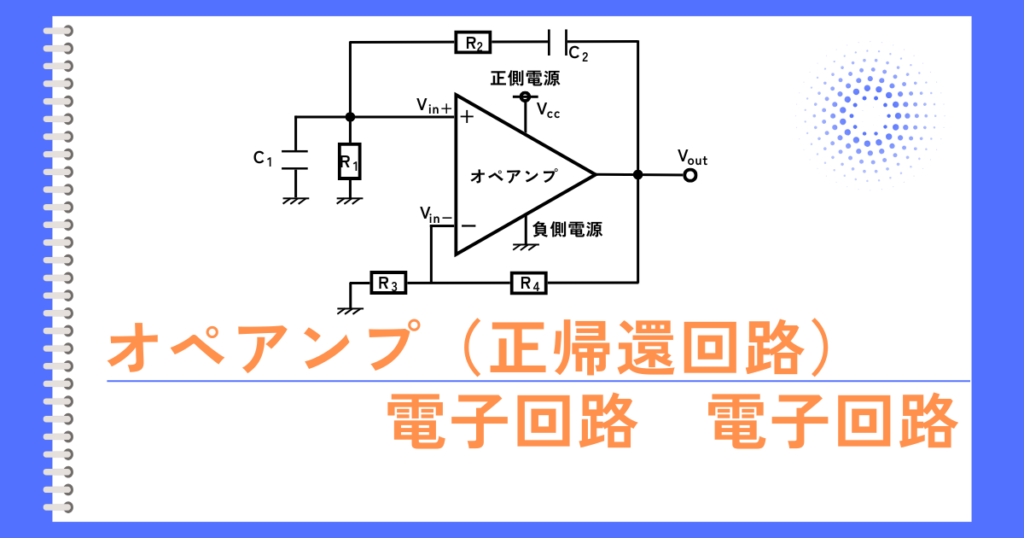
ポジティブフィードバックとは、出力電圧\(V_{out}\)を、非反転入力\(V_{in+}\)に戻すようにした回路です。
ポジティブフィードバックを使う回路は、発振回路や、ヒステリシスコンパレータのような少々特殊な回路が多いです。
正帰還による出力飽和
出力\(V_{out}\)が、正側電源電圧、負側電源電圧に張り付いて、これ以上出力信号が増加しない状態を出力飽和と呼びます。
出力飽和は、あまり望ましくないことが多いですが、ヒステリシスコンパレータは出力飽和になることを利用した回路です。
2つの入力の電位差\(V_e\)は、反転入力\(V_{in-}\)、非反転入力\(V_{in+}\)としたとき、
\(V_e=V_{in+}-V_{in-}\)
です。
出力電圧\(V_{out}\)は、利得を\(A[dB]\)としたとき、
\(V_{out}=AV_e\)
です。
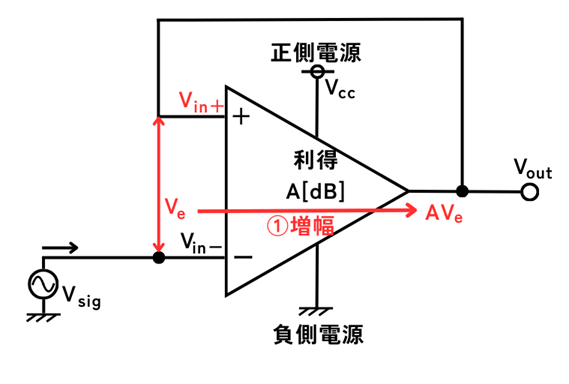
①入力の電位差\(V_e\)を\(A[dB]\)増幅する。
\(V_{out}=AV_e\)
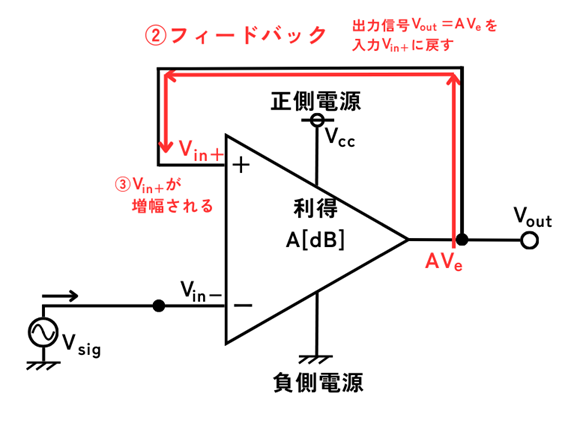
②増幅された出力\(V_{out}\)を、\(V_{in+}\)にフィードバックする。
③\(V_{in+}\)が増幅される。
\(V_{in+}=V_{out}\)
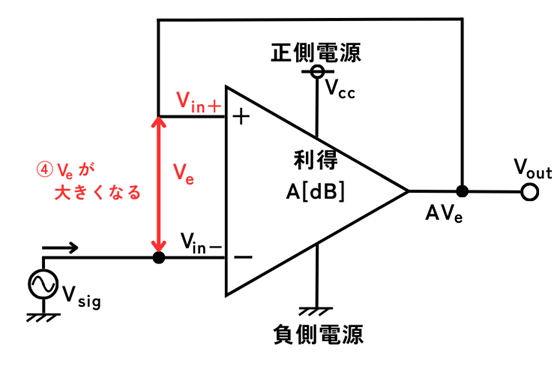
④増幅された\(V_{in+}\)によって、入力の電位差\(V_e\)が大きくなる。
\(V_e=V_{in+}-V_{in-}\)
⑤ ①~④が繰り返される。その結果、
\(V_{in+}>V_{in-}\)の場合
\(V_{out}=+\)側の電源電圧となる。(+側の増幅の限界)
\(V_{in+}<V_{in-}\)の場合
\(V_{out}=-\)側の電源電圧となる。(-側の増幅の限界)
以上のことから、飽和が起きます。
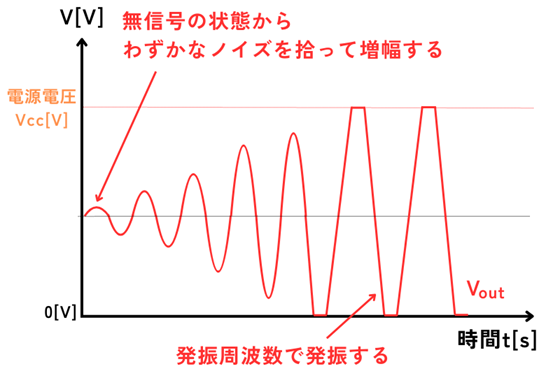
発振動作
発振とは、特定の条件が満たされたとき、特定の周波数で持続的に出力波形を発生させる現象を指します。回路中に入力信号が入力されなくても、出力波形を出し続けることが出来るため、様々な回路で応用されます。
様々な構成で作られる発振回路があります。本ページ内では、ウィーンブリッジ発振回路を紹介します。
ループ利得\(AH\)が次の2つの条件を満たすことが発振条件です。
振幅条件:\(Re(AH)>1\)
周波数条件:\(Im(AH)=0\)
発振動作の振幅条件
次のような、オペアンプの正帰還回路を考えます。
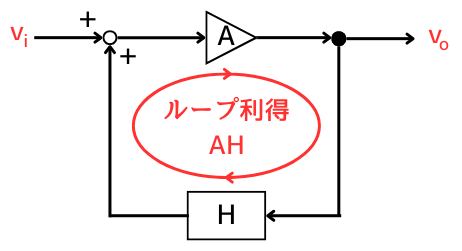
\(A\)はオペアンプの電圧利得で、\(H\)は帰還率です。
出力\(v_o\)が帰還率\(H\)倍した後、オペアンプで\(A\)倍されて帰ってくると、\(v_o\)は\(AH\)倍されます。
この\(AH\)は帰還回路を一巡したときの利得であり、ループ利得と呼びます。
ループ利得\(AH=1\)のとき、出力電圧\(v_0\)が帰還して増幅された結果が1倍となるので、減衰も、増幅もしません。
ループ利得\(AH>1\)のとき、出力電圧\(v_0\)が帰還して増幅された結果が1倍よりも大きくなるので、増幅していきます。
出力電圧\(v_o\)は、飽和するまで増幅するため、\(AH≧1\)のときに発振します。
発振動作の周波数条件
\(Im(AH)\)は、ループ利得\(AH\)の虚数部分です。
ループ利得\(AH\)の虚数部分が0でないとき、つまり、\(Im(AH≠0)\)のときは、ループする信号の位相が位相差角分ずれていきます。
その結果、ループ信号は反転し、減衰させる方向に働いてしまうため、\(Im(AH≠0)\)のときは発振することが出来ません。
そのため、\(Im(AH=0)\)が発振条件となります。
フィードバック回路の計算
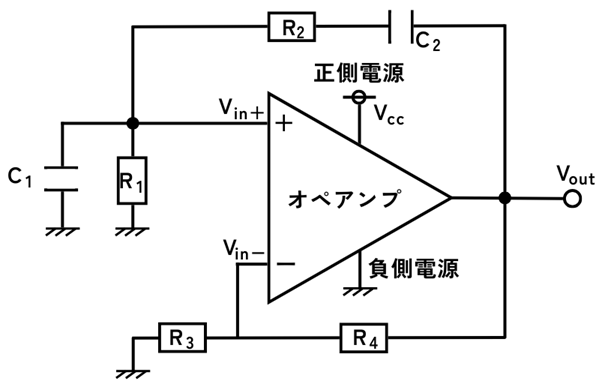
ウィーンブリッジ発振回路
回路の概要
動作概要
発振条件を満たすとき、次の特定の発振周波数で出力\(V_{out}\)が発振する回路です。
発振周波数
\(\displaystyle f[Hz]=\frac{1}{2π \sqrt{C_1C_2R_1R_2}}\)
発振条件
\(\displaystyle 1+\frac{C_1}{C_2}+\frac{R_2}{R_1}=\frac{R_3+R_4}{R_3}\)
回路構成と動作例
ウィーンブリッジ回路の回路構成
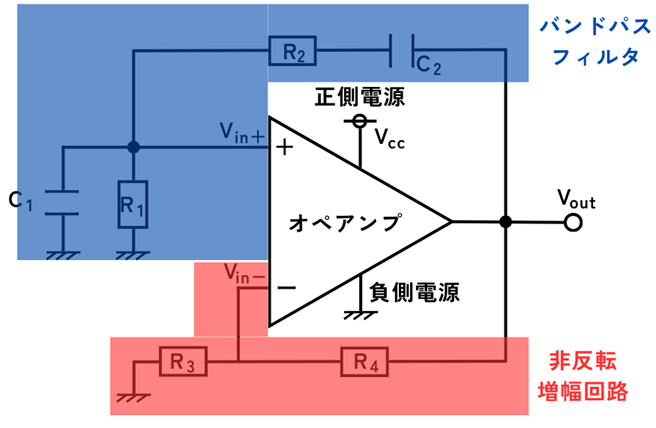
次の①・②の二つの回路から構成されます。
①正帰還回路(バンドパスフィルタ)
オペアンプの出力\(V_{out}\)を、\(R_1\)、\(R_2\)、\(C_1\)、\(C_2\)からなるバンドパスフィルタを通し、非反転入力\(V_{in+}\)に正帰還した回路
②負帰還回路(非反転増幅回路)
オペアンプの出力\(V_{out}\)を、\(R_3\)、\(R_4\)を通した非反転増幅回路を反転入力\(V_{in-}\)に負帰還した回路
ウィーンブリッジ回路の解析
(1)正帰還回路(バンドパスフィルタ)の解析
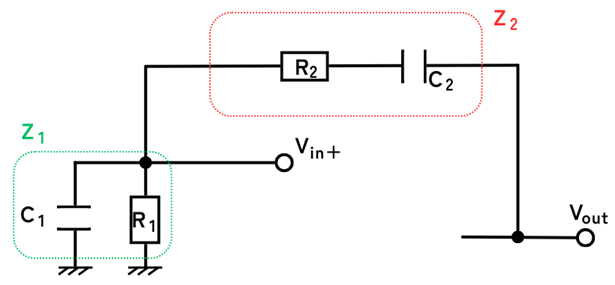
\(V_{out}\)からバンドパスフィルタを通って正帰還した、\(V_{in+}\)の信号について解析します。
まずは、合成インピーダンス\(Z_1\)、\(Z_2\)を求めます。
\(\displaystyle \frac{1}{Z_1}=\frac{1}{R_1}+jωC_1\) ⇔ \(\displaystyle Z_1=\frac{R_1}{1+jωC_1R_1}\)
\(\displaystyle Z_2=R_2+\frac{1}{jωC_2}\)
次に、\(V_{in+}\)を求めます。
\(\displaystyle V_{in+}=\frac{Z_1}{Z_1+Z_2}V_{out}=\frac{\frac{R_1}{1+jωC_1R_1}}{\frac{R_1}{1+jωC_1R_1}+\frac{1}{jωC_2}+R_2}V_{out}\)
⇔\(\displaystyle V_{in+}=\frac{R_1}{R_1+\frac{1+jωC_1R_1}{jωC_2}+R_2+jωC_1R_1R_2}V_{out}\)
⇔\(\displaystyle V_{in+}=\frac{jωC_2R_1}{jωC_2R_1+1+jωC_1R_1+jωC_2R_2-ω^2C_1C_2R_1R_2}V_{out}\)
⇔\(\displaystyle V_{in+}=\frac{jωC_2R_1}{(1-ω^2C_1C_2R_1R_2)+jω(C_1R_1+C_2R_1+C_2R_2)}V_{out}\)
⇔\(\displaystyle V_{in+}=\frac{1}{\frac{1-ω^2C_1C_2R_1R_2}{jωC_2R_1}+\frac{C_1R_1+C_2R_1+C_2R_2}{C_2R_1}}V_{out}\)
⇔\(\displaystyle V_{in+}=\frac{1}{j(ωC_1R_2-\frac{1}{ωC_2R_1})+(1+\frac{C_1}{C_2}+\frac{R_2}{R_1})}V_{out}\) …①
(2)負帰還回路(非反転増幅回路)の解析
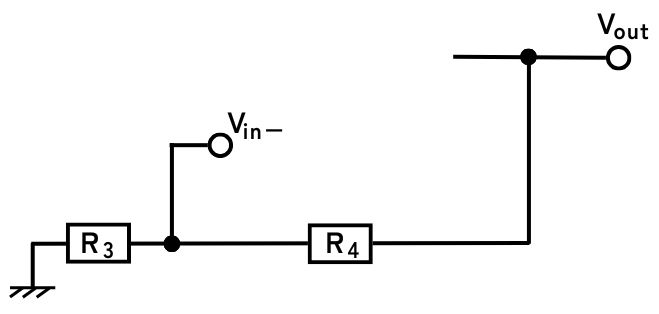
\(V_{out}\)から非反転増幅回路を通って負帰還した\(V_{in-}\)の信号について解析します。
\(\displaystyle V_{in-}=\frac{R_3}{R_3+R_4}V_{out}\) …②
(3)発振周波数の導出
発振周波数は①式の虚数項が0になる周波数です。したがって、
\(\displaystyle ωC_1R_2-\frac{1}{ωC_2R_1}=0\) ⇔ \(\displaystyle ω=\frac{1}{\sqrt{C_1C_2R_1R_2}}\)
\(ω=2πf\)なので、発振周波数は次のように求まります。
\(\displaystyle f=\frac{1}{2π\sqrt{C_1C_2R_1R_2}}\)
(4)発振条件の導出
発振条件は、①式=②式です。
(3)で求めた、虚数項が0となる条件を満たすとき、①式の実数項=②式となれば発振条件が満たせます。
この実数項の条件を計算すると、次のように求まります。
\(\displaystyle \frac{1}{1+\frac{C_1}{C_2}+\frac{R_2}{R_1}}V_{out}=\frac{R_3}{R_3+R_4}V_{out}\)
⇔\(\displaystyle 1+\frac{C_1}{C_2}+\frac{R_2}{R_1}=\frac{R_3+R_4}{R_3}\)
以上より、ウィーンブリッジ発振回路の発振周波数と発振条件が導出できました。
(5)条件の追加(\(R=R_1=R_2\)、\(C=C_1=C_2\)のとき)
この時、発振周波数と発振条件は次のようになります。
発振周波数
\(\displaystyle ω=\frac{1}{CR}\)
発振条件
\(\displaystyle 1+\frac{C_1}{C_2}+\frac{R_2}{R_1}=1+1+1=\frac{R_3+R_4}{R_3}\)
⇔ \(R_4=2R_3\)
ヒステリシスコンパレータ
コンパレータとは
コンパレータは、比較器とも呼ばれ、
\(V_{in+}>V_{in-}\)のとき、\(V_{out}=V_{cc}\)
\(V_{in+}<V_{in-}\)のとき、\(V_{out}=V_{dd}\)
となる動作をします。
コンパレータとオペアンプは、かなり似た素子です。
大きな違いは、オペアンプは帰還することを前提に設計されているのに対し、コンパレータは負帰還しないことを前提に設計されていることから、位相補償回路が不要となる点です。
位相補償回路は動作を遅くさせる回路であるため、これが無いことで、オペアンプに比べて高速で動作します。
他にも、様々な違いはありますが、低い周波数の回路では、オペアンプをコンパレータとして使用することが可能な場合もあります。注意深く設計する必要があるため、あまり推奨はされませんが。
ヒステリシスコンパレータの概要
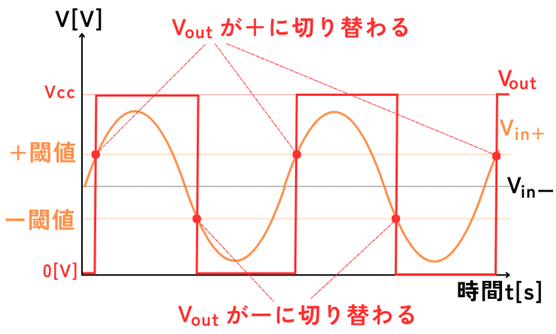
ヒステリシスコンパレータとは、ヒステリシス動作をするコンパレータです。
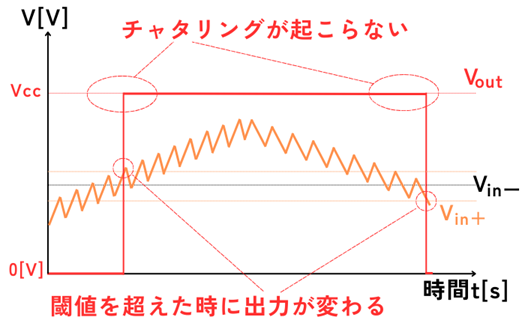
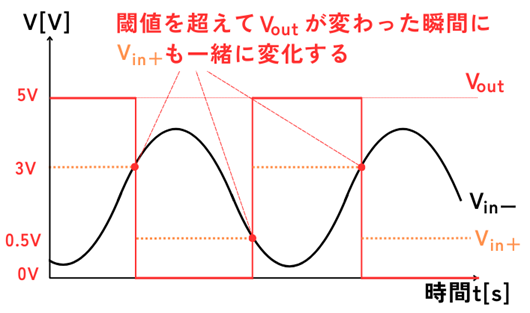
ヒステリシスとは、出力\(V_{out}\)の2つ状態のそれぞれに、切り替わるための閾値を用意することです。
\(V_{out}\)が\(0V→V_{cc}\)に切り替わるタイミングは、+閾値を超えた時に切り替わります。
\(V_{out}\)が\(V_{cc}→0V\)に切り替わるタイミングは、-閾値を超えた時に切り替わります。
ヒステリシスコンパレータの動作を示すと、次の図の通りになります。
ヒステリシスコンパレータを使う理由
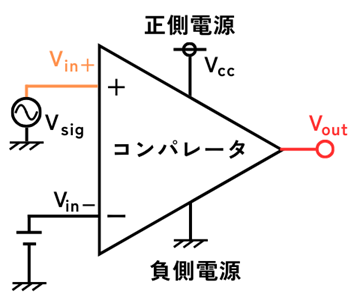
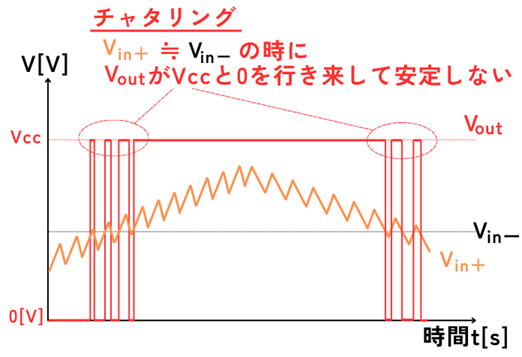
ヒステリシスコンパレータを使う理由は、チャタリングを防ぐためです。
チャタリングとは、入力が\(V_{in+}≒V_{in-}\)のときに、出力が\(V_{out}=V_{cc}\)、\(V_{out}=V_{dd}\)を激しく行ったり来たりしてしまう現象です。
コンパレータを使用した場合のチャタリングの例です。
ヒステリシスコンパレータに変更すると、次のようになり、チャタリングが解消されます。
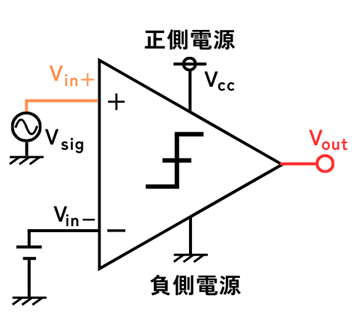
ヒステリシスコンパレータの回路構成
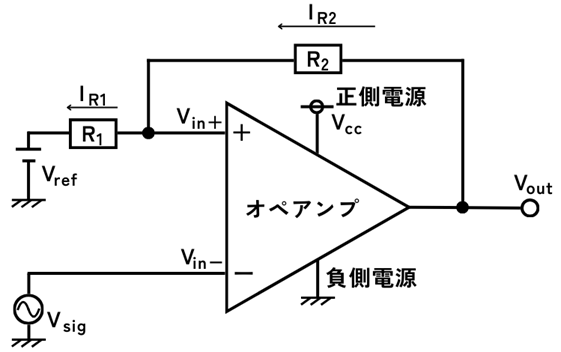
オペアンプの出力\(V_{out}\)を増幅回路のように抵抗\(R_2\)を通して非反転入力\(V_{in+}\)にフィードバックします。
また、非反転入力\(V_{in+}\)から抵抗\(R_1\)を通してリファレンス電圧\(V_{ref}\)にも接続します。
リファレンス電圧\(V_{ref}\)は、抵抗分圧や、DAC(デジタルアナログコンバータ)等を使用して作られます。
ヒステリシスコンパレータの回路解析
ヒステリシスコンパレータの動作を示すために、回路を解析していきます。
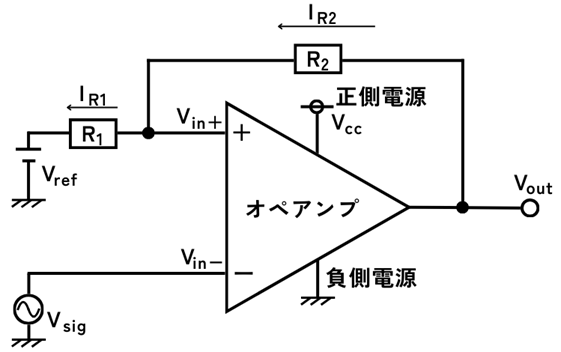
図の\(I_{R1}\)、\(I_{R2}\)を求めます。
\(\displaystyle I_{R1}=\frac{V_{in+}-V_{ref}}{R_1}\)
\(\displaystyle I_{R2}=\frac{V_{out}-V_{in+}}{R_2}\)
\(I_{R1}=I_{R2}\)なので、
\(\displaystyle \frac{V_{in+}-V_{ref}}{R_1}=\frac{V_{out}-V_{in+}}{R_2}\)
⇔\(\displaystyle (R_1+R_2)V_{in+}=R_1V_{out}+R_2V_{ref}\)
⇔\(\displaystyle V_{in+}=\frac{R_1V_{out}+R_2V_{ref}}{R_1+R_2}\)
動作の例
回路解析した結果が、実際にどのように動作に影響を与えるか示していきます。
オペアンプの正側電源\(V_{cc}=5V\)、負側電源\(V_{dd}=0V\)、リファレンス電圧\(V_{ref}=1V\)、抵抗\(R_1=R_2=1kΩ\)とします。この時の動作例を示してみます。
二つの動作モードがあります。
①\(V_{in+}>V_{in-}\)のとき
\(V_{out}=V_{cc}=5V\)となります。
この時の\(V_{in+}\)の電圧は、
\(\displaystyle V_{in+}=\frac{R_1V_{out}+R_2V_{ref}}{R_1+R_2}=\frac{1000・5+1000・1}{1000+1000}=\frac{6}{2}=3V\)
②\(V_{in+}<V_{in-}\)のとき
\(V_{out}=V_{dd}=0V\)となります。
この時の\(V_{in+}\)の電圧は、
\(\displaystyle V_{in+}=\frac{R_1V_{out}+R_2V_{ref}}{R_1+R_2}=\frac{1000・0+1000・1}{1000+1000}=\frac{1}{2}=0.5V\)
入出力の関係は、次の図のようになります。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント