概要
テブナンの定理とRC回路の過渡応答が複合された問題です。
複合問題なため、ぱっと見難しそうですが、テブナンの定理の問題としても、RCの過渡応答の問題としても、個々の難易度は初歩的です。
キーワード
RC回路、過渡応答、時定数、定常状態、テブナンの定理
問題
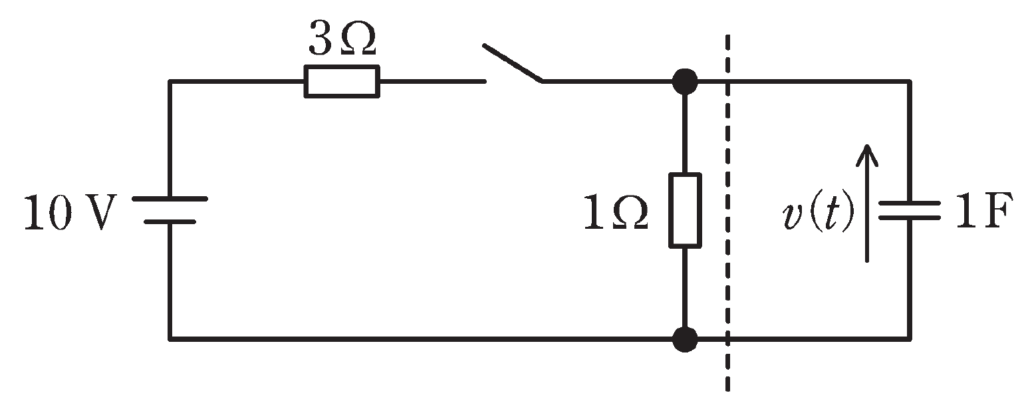
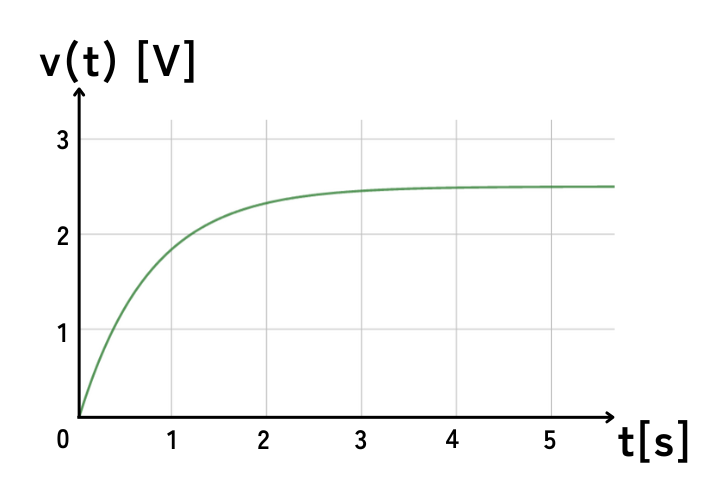
図の回路のスイッチを閉じたあとの電圧\(v(t)\)の波形を考える。
破線から左側にテブナンの定理を適用することで、回路の時定数[s]と\(v(t)\)の最終値[V]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、初めスイッチは開いており、回路は定常状態にあったとする。
| 時定数[s] | 最終値[V] | |
| (1) | 0.75 | 10 |
| (2) | 0.75 | 2.5 |
| (3) | 4 | 2.5 |
| (4) | 1 | 10 |
| (5) | 1 | 0 |
答え
(2)
解説テキスト リンク
回答解説
回答の流れ
(a)問題の解答を行う
①テブナンの定理を使って回路を書き直す
②RC回路の\(v(t)\)について微分方程式を立てる
③過渡状態を解析して時定数を導出する
④定常状態を解析する
————–ここまでで回答可能————–
【蛇足】\(v(t)\)の過渡応答の式を導出する
⑤初期状態を解析する
⑥\(v(t)\)の一般解を求める

(a)問題の解答を行う
①テブナンの定理を使って回路を書き直す
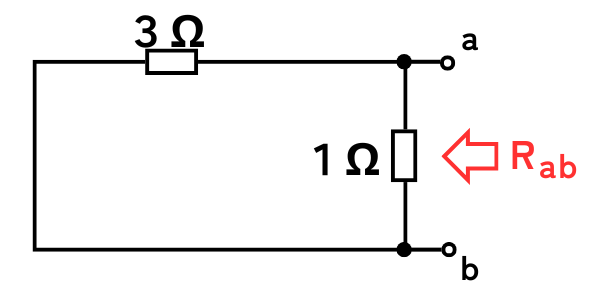
破線から左側を見た抵抗\(R_{ab}\)を求めます。
\(\frac{1}{R_{ab}}=\frac{1}{3}+\frac{1}{1}\)
⇔\(R_{ab}=\frac{3}{4}=0.75Ω\)
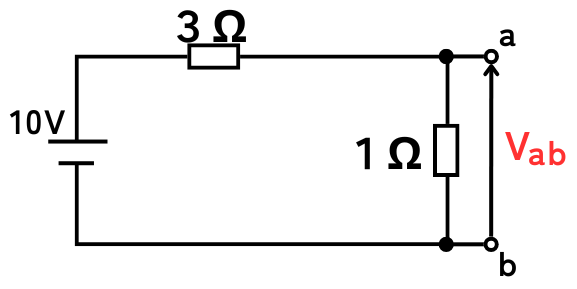
破線の端子電圧\(V_{ab}\)を求めます。
\(V_{ab}=\frac{1}{1+3}10=2.5V\)
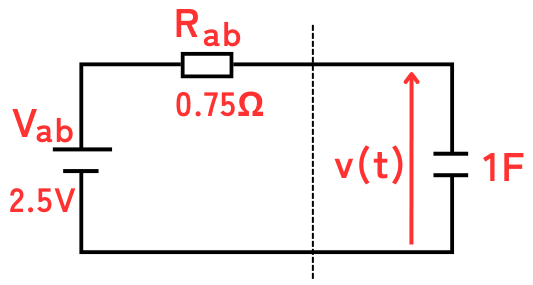
テブナン等価回路に書き直すと左図のようになります。
②RC回路の\(v(t)\)について微分方程式を立てる

回路中を流れる電流を\(i[A]\)とします。
電流の定義式から、次の電流と電荷の関係式が出せます。
\(i=\frac{dq}{dt}\)
コンデンサの電荷、静電容量、電圧の関係式から
\(q=Cv(t)\)
電流と電荷の関係式に代入すると、
\(i=C \frac{dv(t)}{dt}\)
回路の方程式は、次式となります。
\(V_{ab}=R_{ab}i+v(t)\)
⇔ \(V_{ab}=CR_{ab}\frac{dv(t)}{dt}+v(t)\)
③過渡状態を解析して時定数を導出する
コンデンサ電圧の過渡解を\(v_t(t)\)とします。
\(v_t(t)=ke^{-st}\)
としたとき、
\(\frac{dv_t(t)}{dt}=-ske^{-st}\)
過渡解を求める方程式は、
\(0=ke^{-st}-CR_{ab}ske^{-st}=(1-CR_{ab}s)ke^{-st}\)
上式が成り立つ条件は、
\(s=\frac{1}{CR_{ab}}\)
です。
時定数\(τ\)は、過渡解の式が\(e^{-1}\)となるときの時間であるため、
\(sτ=1\)
⇔ \(τ=\frac{1}{s}=CR_{ab}=1・0.75=0.75[s]\)
したがって、時定数\(τ=0.75s\)と求まりました。
④定常状態を解析する
コンデンサは、テブナン等価回路の電源電圧\(V_{ab}=2.5V\)まで充電されます。
コンデンサ電圧の最終値である定常解は、\(t=∞\)秒立った時の電圧として考えられるので、\(v_s(∞)=2.5V\)と表せます。
以上より、
(2)時定数\(τ[s]=0.75\)、最終値\(v(∞)=2.5\)と求まりました。
【蛇足】\(v(t)\)の過渡応答の式を導出する
既に問いに対する解は求まりましたが、一般解を求めたらどのような式になるかを示します。
⑤初期状態を解析する
コンデンサの初期電圧は、\(v(0)=0V\)です。
したがって、
\(v(0)=v_t(0)+v_s(∞)=ke^0+2.5=k+2.5=0\)
⇔ \(k=-2.5\)
よって、過渡解\(v_t(t)\)が、次のように求まります。
\(\displaystyle v_t(t)=-2.5e^{-\frac{1}{0.75}t}\)
⑥\(v(t)\)の一般解を求める
\(\displaystyle v(t)=v_t(t)+v_s(∞)=-2.5e^{-\frac{1}{0.75}t}+2.5=2.5(1-e^{-\frac{1}{0.75}t})\)
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和2年度 第三種電気主任技術者試験 理論科目A問題問10
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント