交流回路の理論において、三角関数は切っても切り離すことはできません。
そして、交流電圧・電流の実効値を求めるような面倒くさい計算は、加法定理を使って式を分解する必要が出てきます。
三角関数に関する基本公式と、導出と、電験三種での使用頻度をまとめました。
三角関数の基本式
| 公式 | 使用頻度 | 暗記 |
| \(sin^2θ+cos^2θ=1\) | 最重要。絶対使う。 | 必須 |
| \(\displaystyle tanθ=\frac{sinθ}{cosθ}\) | 時々使う | 必須 |
【補足】
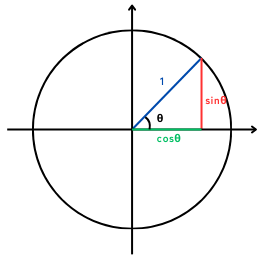
\(sin^2θ+cos^2θ=1\)は三平方の定理で導かれます。
\(\displaystyle tanθ=\frac{sinθ}{cosθ}\)は、∠θの傾きを表します。
| 公式 | 使用頻度 | 暗記する価値 |
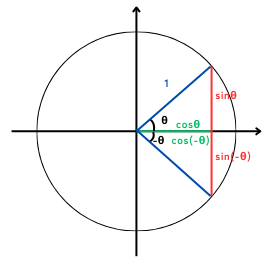
| \(sin(-θ)=-sinθ\) | 時々使う | 必要ない。 |
| \(cos(-θ)=cosθ\) | 時々使う | 必要ない。 |
| 公式 | 使用頻度 | 暗記 |
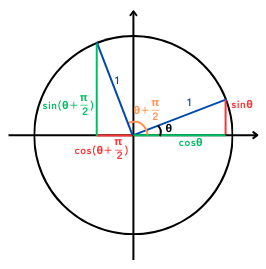
| \(\displaystyle sin(θ+\frac{π}{2})=cosθ\) | 時々使う | 必要ない。 |
| \(\displaystyle cos(θ+\frac{π}{2})=-sinθ\) | 時々使う | 必要ない。 |
| 公式 | 使用頻度 | 暗記 |
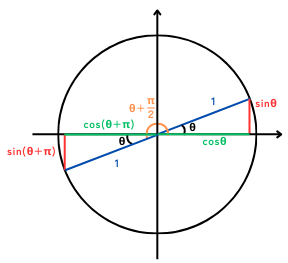
| \(\displaystyle sin(θ+π)=-sinθ\) | 時々使う | 必要ない。 |
| \(\displaystyle cos(θ+π)=-cosθ\) | 時々使う | 必要ない。 |
加法定理
加法定理
角の加算\(α+β\)
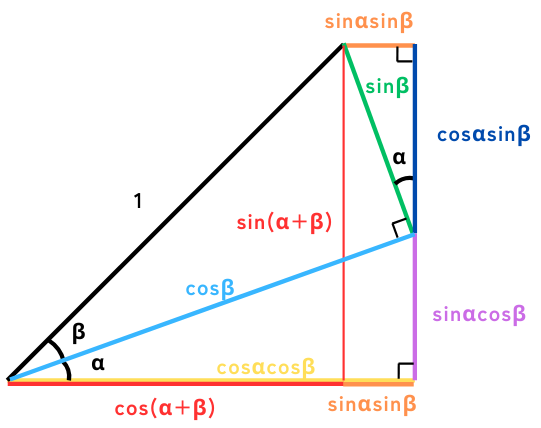
| 公式 | 使用頻度 | 暗記する価値 |
| \(sin(α+β)=sinα・cosβ+cosα・sinβ\) | 交流で使う | 必要 |
| \(cos(α+β)=cosα・cosβ-sinα・sinβ\) | 交流で使う | 必要 |
角の減算\(α-β\)
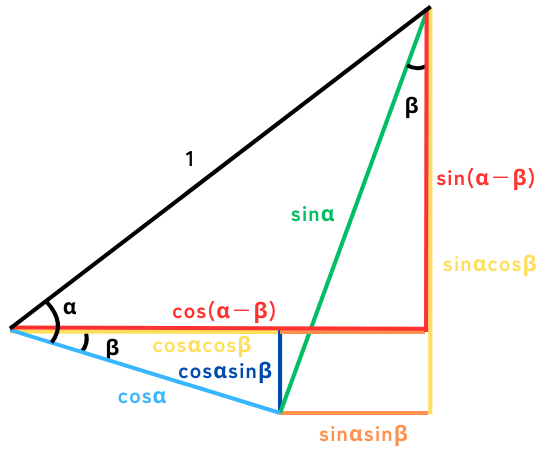
| 公式 | 使用頻度 | 暗記する価値 |
| \(sin(α-β)=sinα・cosβ-cosα・sinβ\) | 交流で使う | 必要 |
| \(cos(α-β)=cosα・cosβ+sinα・sinβ\) | 交流で使う | 必要 |
加法定理の逆変換
| 公式 | 使用頻度 | 暗記する価値 |
| \(\displaystyle sinα・sinβ=\frac{cos(α-β)-cos(α+β)}{2}\) | 時々使う | なし。 導出出来れば良い。 |
| \(\displaystyle cosα・cosβ=\frac{cos(α-β)+cos(α+β)}{2}\) | 時々使う | なし。 導出出来れば良い。 |
| \(\displaystyle sinα・cosβ=\frac{sin(α+β)+sin(α-β)}{2}\) | 時々使う | なし。 導出出来れば良い。 |
| \(\displaystyle cosα・sinβ=\frac{sin(α+β)-sin(α-β)}{2}\) | 時々使う | なし。 導出出来れば良い。 |
加法定理の逆変換の導出
\(\displaystyle sinα・sinβ=\frac{cos(α-β)-cos(α+β)}{2}\) …(A)
\(\displaystyle cosα・cosβ=\frac{cos(α-β)+cos(α+β)}{2}\) …(B)の導出
\(cos(α-β)=cosα・cosβ+sinα・sinβ\) …①
\(cos(α+β)=cosα・cosβ-sinα・sinβ\) …②
①-②より、
\(2sinα・sinβ=cos(α-β)-cos(α+β)\)
⇔\(\displaystyle sinα・sinβ=\frac{cos(α-β)-cos(α+β)}{2}\)
①+②より、
\(2cosα・cosβ=cos(α-β)+cos(α+β)\)
⇔\(\displaystyle cosα・cosβ=\frac{cos(α-β)+cos(α+β)}{2}\)
\(\displaystyle sinα・sinβ=\frac{cos(α-β)-cos(α+β)}{2}\) …(C)
\(\displaystyle cosα・cosβ=\frac{cos(α-β)+cos(α+β)}{2}\) …(D)の導出
\(sin(α+β)=sinα・cosβ+cosα・sinβ\) …③
\(sin(α-β)=sinα・cosβ-cosα・sinβ\) …④
③+④より、
\(2sinα・cosβ=sin(α+β)+sin(α-β)\)
⇔\(\displaystyle sinα・cosβ=\frac{sin(α+β)+sin(α-β)}{2}\)
③-④より、
\(2cosα・sinβ=sin(α+β)-sin(α-β)\)
⇔\(\displaystyle cosα・sinβ=\frac{sin(α+β)-sin(α-β)}{2}\)
倍角の公式
| 公式 | 使用頻度 | 暗記する価値 |
| \(sin2α=2sinα・cosα\) | 交流で使う | 無い。導出すれば良い。 |
| \(cos2α=cos^2α-sin^2α\) | 交流で使う | 無い。導出すれば良い。 |
倍角の公式の導出
\(sin2α=2sinα・cosα\)の導出
加法定理の式\(sin(α+β)=sinα・cosβ+cosα・sinβ\)の式に対し、
\(α=β\)とすると、
\(sin(α+α)=sinα・cosα+cosα・sinα=2sinα・cosα\)
\(cos2α=cos^2α-sin^2α\)の導出
加法定理の式\(cos(α+β)=cosα・cosβ+sinα・sinβ\)の式に対し、
\(α=β\)とすると、
\(cos(α+α)=cosα・cosα-sinα・sinα=cos^2α-sin^2α\)
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント