インピーダンス１（交流回路のオームの法則）

インピーダンスの関連式　一覧

交流のオームの法則
\(V=IZ\)

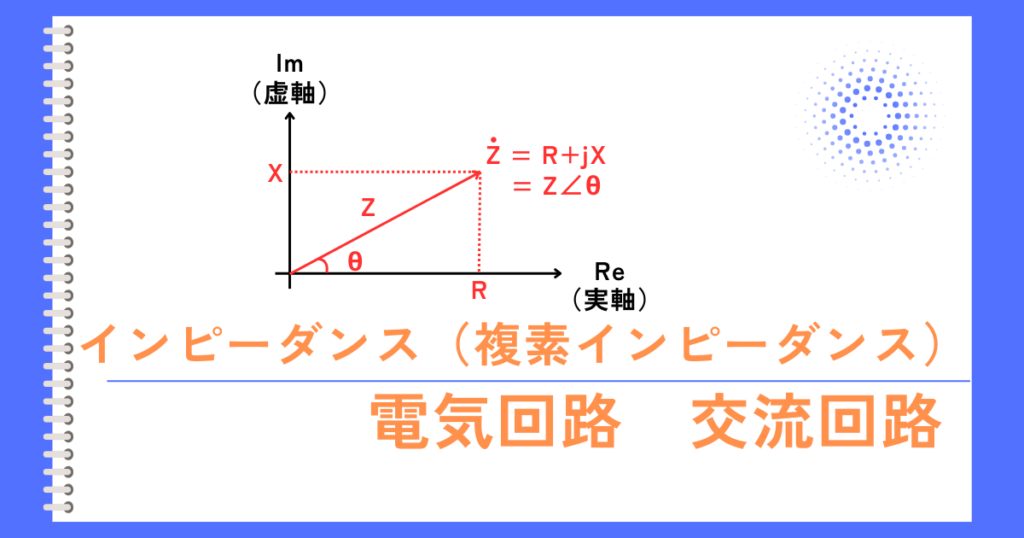
インピーダンス\(Z[Ω]\)と、抵抗\(R[Ω]\)・リアクタンス\(X[Ω]\)の関係式
\(Z=R+jX\)

リアクタンス\(X[Ω]\)と、コイルの誘導性リアクタンス\(X_L[Ω]\)、コンデンサの容量性リアクタンス\(X_C[Ω]\)の関係式
\(X=X_L-X_C\)

周波数\(f[Hz]\)と角周波数\(ω[rad/s]\)の関係式
\(ω=2πf\)

コイルの誘導性リアクタンス\(X_L[Ω]\)と、インダクタンス\(L[H]\)、周波数\(f[Hz]\)・角周波数\(ω[rad/s]\)の関係式
\(X_L=2πfL\)
\(X_L=ωL\)

コンデンサの容量性リアクタンス\(X_C[Ω]\)と、静電容量\(C[F]\)、周波数\(f[Hz]\)・角周波数\(ω[rad/s]\)の関係式
\(\displaystyle X_C=\frac{1}{2πfC}\)
\(\displaystyle X_C=\frac{1}{ωC}\)

　

インピーダンス\(Z\)

回路に直流電流が流れる場合は、電気抵抗が電流を流れにくくします。

回路に交流電流が流れる場合は、電流を流れにくくするのは電気抵抗だけでなく、電流の変化によって生じる電磁界も電流が流れにくくします。
電気抵抗による影響をレジスタンスと呼ぶのに対し、電磁界による影響をリアクタンスと呼びます。
電気抵抗とリアクタンスの影響をまとめたのがインピーダンスです。

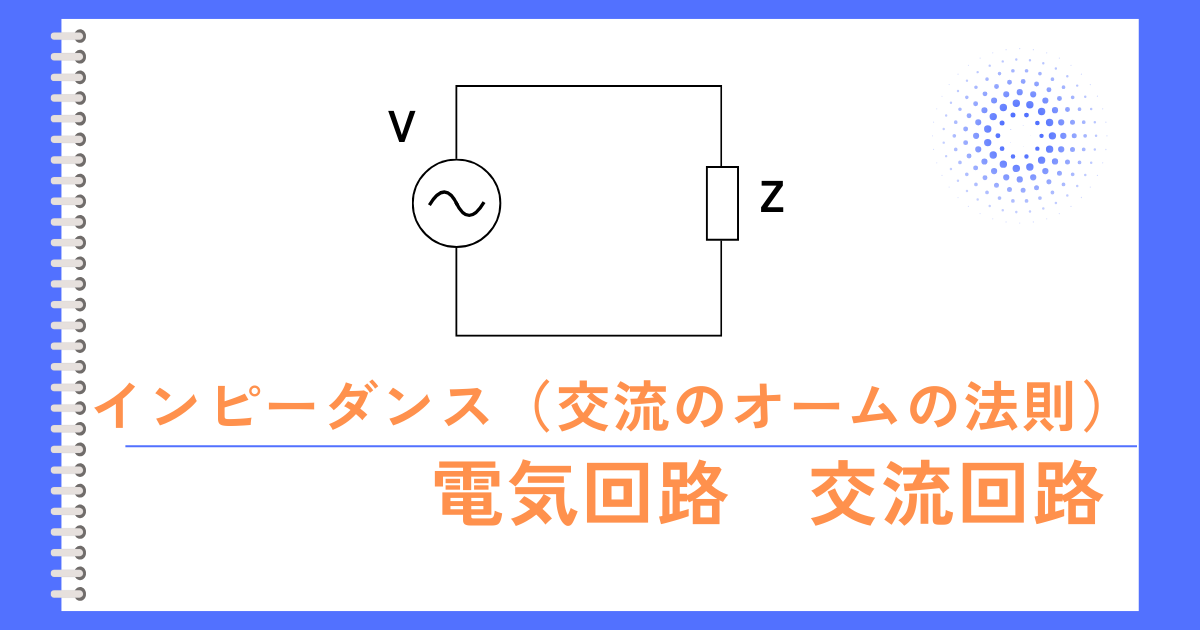
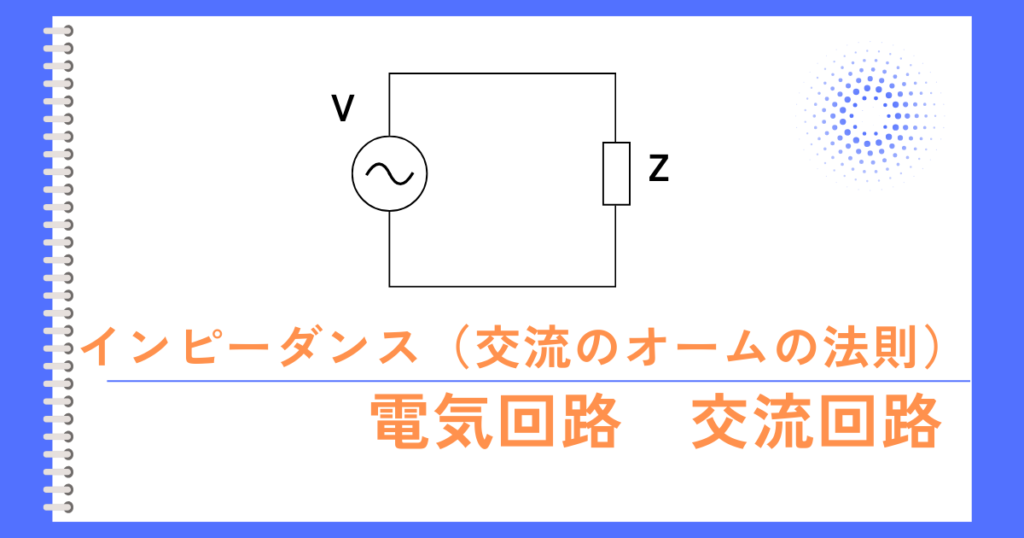
インピーダンス\(Z[Ω]\)には、直流回路のように
オームの法則\(V=IZ\)がなりたちます。

　

　

電気抵抗\(R[Ω]\)

インピーダンスの項目でも前述した通り、電気抵抗\(R\)は、電気の流れの通しにくさを表します。
交流においてもオームの法則は成り立ちます。

オームの法則　\(V=IR\)

電気抵抗\(R\)が、後述するリアクタンス\(X\)と大きく違う点は、
・周波数に依存せず、一定の値である。
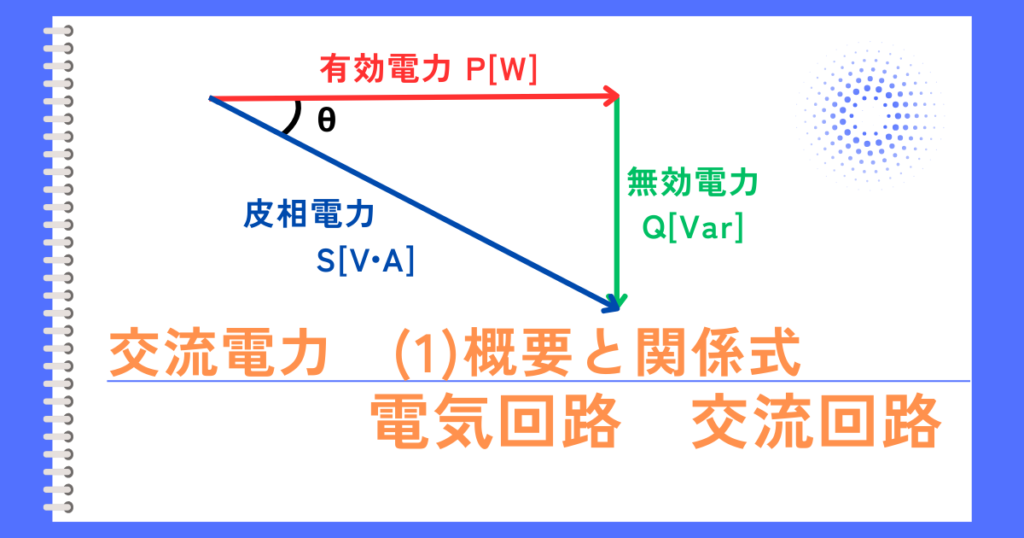
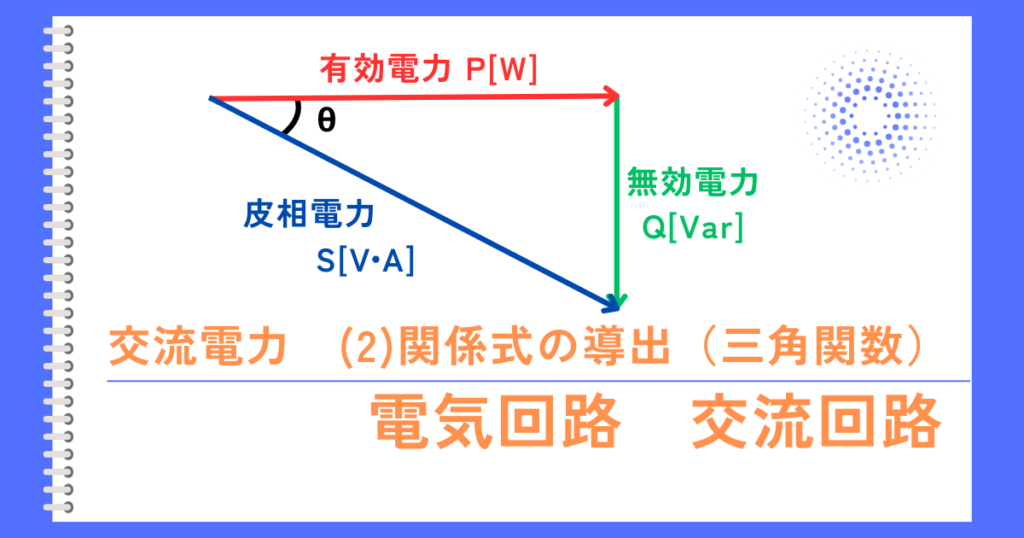
・電気抵抗で消費する電力は、有効電力\(P[W]\)と呼びます。
　有効電力は、電気エネルギーを他のエネルギーに変換した量を表します。
　抵抗器：電気エネルギー　⇒　熱エネルギー
　電動機：電気エネルギー　⇒　運動エネルギー

　

リアクタンス\(X[Ω]\)

電流を妨げるリアクタンス\(X\)には２種類あります。
コイルが持つ誘導性リアクタンス\(X_L\)と、コンデンサが持つ容量性リアクタンス\(X_C\)です。

　

誘導性リアクタンス\(X_L[Ω]\)

コイルに交流電源を接続すると、電源電圧から流れる電流の逆向きに自己誘導起電力が生じることによって、電流が流れるのを妨げます。
この電流を妨げるリアクタンスは、疑似的に抵抗と見なすことができ、電気抵抗と同じくオームの法則が成り立ちます。

オームの法則　\(\displaystyle X_L=\frac{V}{I}\)

誘導性リアクタンス\(X_L[Ω]\)、周波数\(f[Hz]\)、角周波数\(ω[rad/s]\)、コイルの自己インダクタンス\(L[H]\)としたとき、次式で表されます。
\(X_L=2πfL\)
⇔\(X_L=ωL\)

周波数\(f[Hz]\)と角周波数\(ω[rad/s]\)の関係は、次式で表されます。
\(ω=2πf\)

以上のことから、誘導性リアクタンス\(X_L\)は、

• 周波数に比例して大きくなる。
• 誘導性リアクタンスの電力\(Q_L[Var]\)は、無効電力と呼びます。
  電気エネルギーをコイルの中に磁気エネルギーとして蓄えるだけであるため、他のエネルギーには変換されません。（エネルギーを消費しない）
• 電圧の位相が、電流の位相に対して進み位相になります。
  誘導性リアクタンスのみ接続された回路の場合、電圧の位相が電流の位相から\(∠θ=\frac{π}{2}[rad]\)進みます。

　

　

容量性リアクタンス\(X_C[Ω]\)

コンデンサに交流電源を接続すると、コンデンサは充放電を行います。コンデンサが充放電の電圧に近づいてくると、電圧が変化する速度は遅くなります。そのため、コンデンサは電圧の変化を妨げます。
電圧の変化が小さくなると、電流も比例して小さくなります。

この電圧を妨げる容量性リアクタンスは、疑似的に抵抗と見なすことができ、電気抵抗と同じくオームの法則が成り立ちます。

オームの法則　\(\displaystyle X_C=\frac{V}{I}\)

容量性リアクタンス\(X_C[Ω]\)、周波数\(f[Hz]\)、角周波数\(ω[rad/s]\)、コンデンサの静電容量\(C[F]\)としたとき、次式で表されます。
\(X_C=\frac{1}{2πfC}\)
⇔\(X_C=\frac{1}{ωC}\)

周波数\(f[Hz]\)と角周波数\(ω[rad/s]\)の関係は、次式で表されます。
\(ω=2πf\)

以上のことから、容量性リアクタンス\(X_C\)は、

• 周波数に比例して小さくなるC
• 容量性リアクタンスの電力\(Q_C[Var]\)は、無効電力と呼びます。
  電気エネルギーをコンデンサの中に静電エネルギーとして蓄えるだけであるため、他のエネルギーには変換されません。（エネルギーを消費しない）
• 電圧の位相が、電流の位相に対して遅れ位相になります。
  容量性リアクタンスのみ接続された回路の場合、電圧の位相が電流の位相から\(∠θ=\frac{π}{2}[rad]\)遅れます。

　

　

　

関連記事（交流回路に関する解説）

　

　　

参考書