公式一覧
自己インダクタンスに蓄えられるエネルギー
\(\displaystyle U=\frac{1}{2}LI^2\)
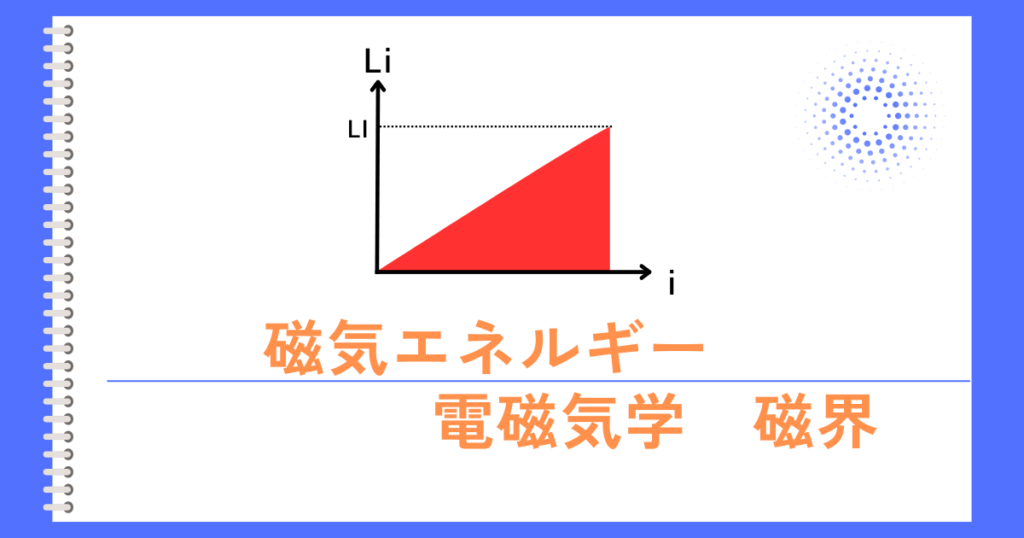
磁気エネルギー
自己インダクタンスに蓄えられるエネルギー
自己インダクタンスに蓄えられるエネルギー
\(\displaystyle U=\frac{1}{2}LI^2\)
コイルに電流が流れているとき、磁気エネルギーがコイルに蓄えられます。
どのようにエネルギーが蓄えられるかというと、コイルに流れる電流が周囲に磁界を作りだすことで、磁界という形で周囲の空間にエネルギーが蓄えられます。
自己インダクタンスに蓄えられるエネルギーの導出
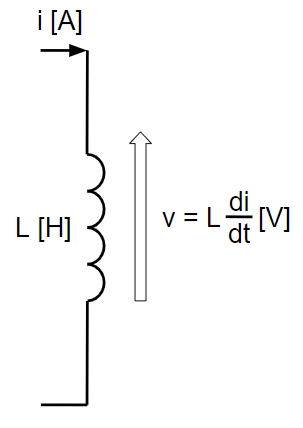
左図のように、自己インダクタンス\(L[H]\)のコイルに、時間変化する電流\(i[A]\)を流した時、コイルに蓄えられるエネルギー\(W[W]\)を考えます。
コイルの電位\(v[V]\)は、次式となります。
(式の導出の参考→自己インダクタンスの解説)
\(\displaystyle v=L\frac{di}{dt}\) …①
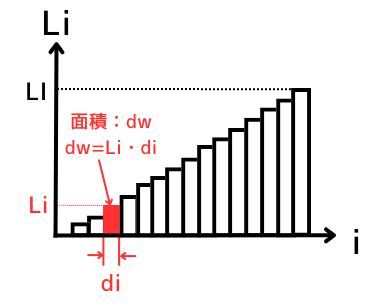
\(\frac{di}{dt}\)は、コイルに流れる電流\(i\)が、\(dt\)秒間に\(di\)だけ変化したことを表します。
次に、電源がコイルに送る電力\(p[W]\)は、
\(\displaystyle p=v・i=\left(L \frac{di}{dt}\right)・i[W]\) …②
\(dt\)秒間にコイルが受取るエネルギー\(dw[W]\)は、
\(\displaystyle dw = p・dt\) …③
③式に①・②式を代入して展開していくと、
\(\displaystyle \begin{eqnarray}
dw &=& p・dt = v・i dt\\
&=& \left(L \frac{di}{dt}\right)・i・dt\\
&=& Li・di …④
\end{eqnarray}\)
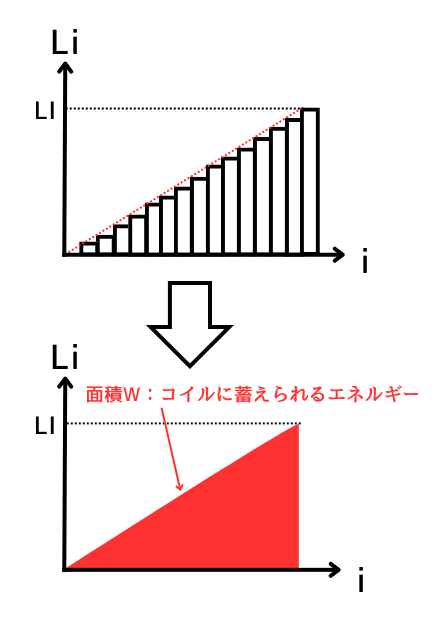
時間変化しなくなり、流れる電流が\(I[A]\)となったときに、コイルの\(L[H]\)が蓄えるエネルギー\(W[J]\)は、④式の電流\(i\)が初期値(\(i=0\))から、定常状態(\(i=I\))になるまでを積分すれば求まります。
\(\displaystyle W=\int_{0}^{I} dw=\int_{0}^{I} L・i・di=L\int_{0}^{I} i・di\)
\(\displaystyle =L\left[\frac{1}{2}i^2\right]_0^I=\frac{1}{2}LI^2[J]\)
以上より、コイルに蓄えられる磁気エネルギーは\(\displaystyle W=\frac{1}{2}LI^2[J]\)です。
過去問
難易度 ★★☆☆☆
| 電験三種 平成21年度 問3 | 磁束鎖交数と磁気エネルギーの計算 |
関連記事(磁界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント