ガウスの法則
ガウスの法則と電界強度E
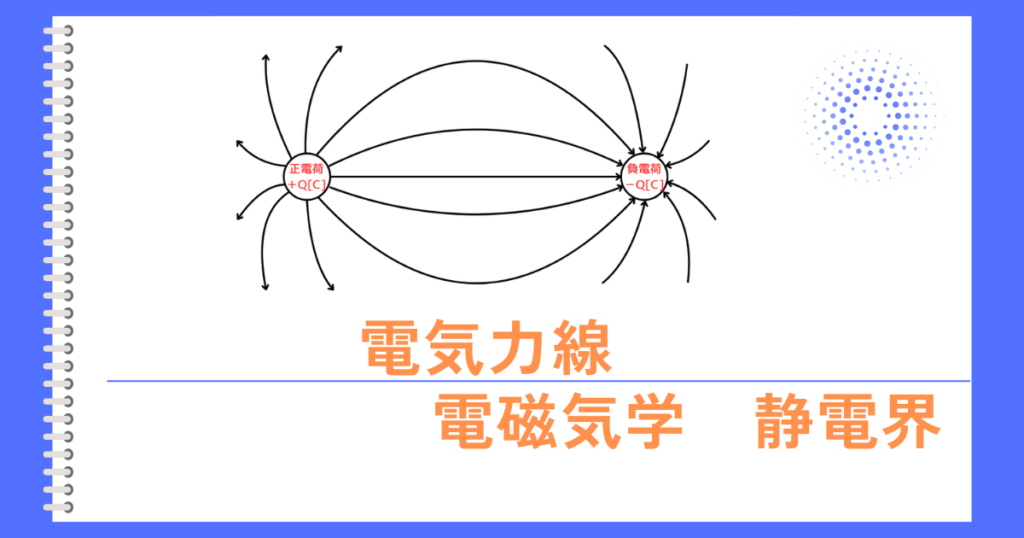
ガウスの法則とは、ある閉曲面\(S\)を垂直に貫いて外へ出る電気力線の総数は、その閉曲面内に含まれる全電荷量に等しいという法則です。
つまり、電荷と電界の関係をあらわす法則です。
ガウスの法則によって表される電荷と電界強度の関係の式は、次式となります。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
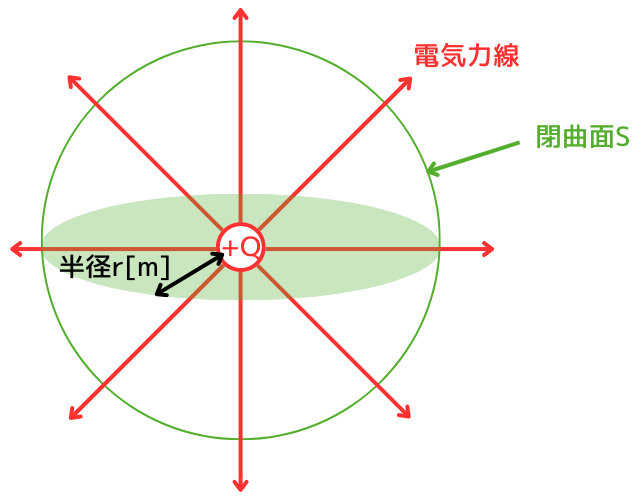
電界強度\(E\)は、左図のように矢印で示されます。そのため、一般式として示す場合は、次式のようにベクトルで示されます。
\(\displaystyle \oint_S \boldsymbol{E}・\boldsymbol{n}dS=\frac{Q}{ε_0}\)
・\(Q[C]\) 閉曲面内部に存在する電荷量
・\(ε_0[F/m]\) 真空の誘電率
・\(E[V/m]\) 電界強度
ガウスの法則の式の意味をざっくり分解していきます。
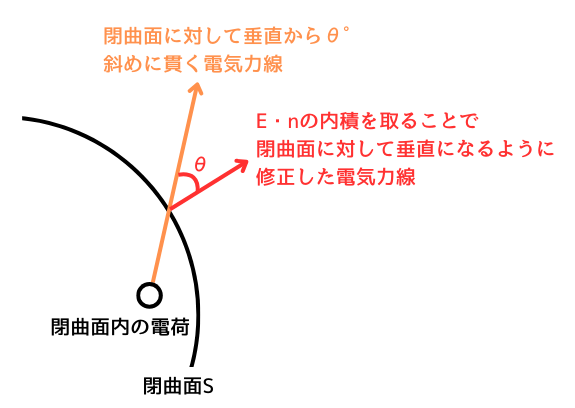
\(\boldsymbol{E}・\boldsymbol{n}\)の概要図
①電気力線が閉曲面を垂直に貫く成分だけ取り出す。
ガウスの法則では、閉曲面を貫く電気力線は、垂直に貫くことが重要です。しかし、閉曲面内に電荷が複数点在している場合は、垂直に貫かない電気力線も存在します。
そこで、電界のベクトル\(\boldsymbol{E}\)と法線ベクトル\(\boldsymbol{n}\)の内積を取り、\(\boldsymbol{E}・\boldsymbol{n}\)とします。
内積を取ることで、閉曲面内の電荷から放出される電気力線から、閉曲面\(S\)を垂直に貫く成分だけを取り出せます。
②閉曲面の全領域に対して計算する。
閉曲面の全ての領域に対して、閉曲面を貫く電気力線を数える必要があります。
そのため、周回積分\(\displaystyle \oint_S dS\)を使うことで、閉曲面\(S\)の全領域を貫く電界のベクトルを数えることができます。
以上、①・②で閉曲面を貫く電気力線を垂直成分のみに換算し、閉曲面の全領域に対して周回積分計算をすることで、ガウスの法則のある閉曲面\(S\)を垂直に貫いて外へ出る電気力線の総数を表現することができました。
上記で説明した通り、電界を厳密に式として表すのであればベクトルの形で式を立てることとなります。しかし、電験三種の試験では、
①電界の大きさだけを考える。
②電界の向きを別途考える。
この2ステップで十分に解答することができるので、電界の大きさだけを考えれば良いです。
そのため、次のように簡単化できます。
\(\displaystyle \oint_S \boldsymbol{E}・\boldsymbol{n}dS=\frac{Q}{ε_0}\) ⇒ \(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
閉曲面\(S\)の面積は、考える場面によって全く異なります。
この考える場面は、次の3パターンがあります。
①点電荷
②線電荷(ケーブルのような直線導体)
③平行平板コンデンサ
この3パターンについて、それぞれ考えて行きます。
点電荷の電界強度E
点電荷の電界強度\(E[V/m]\)は
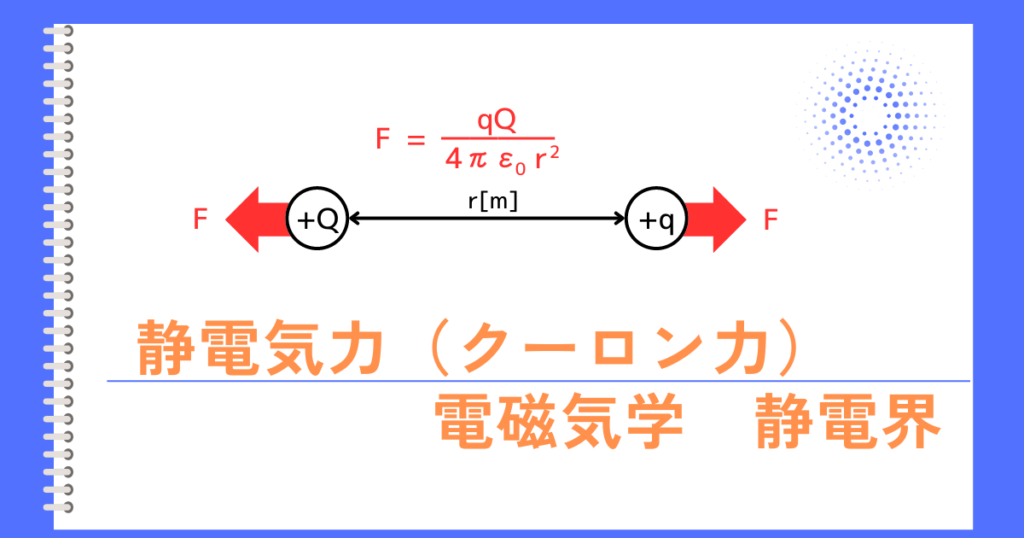
\(\displaystyle E=\frac{Q}{4πε_0r^2}\)

ガウスの法則の式を示します。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
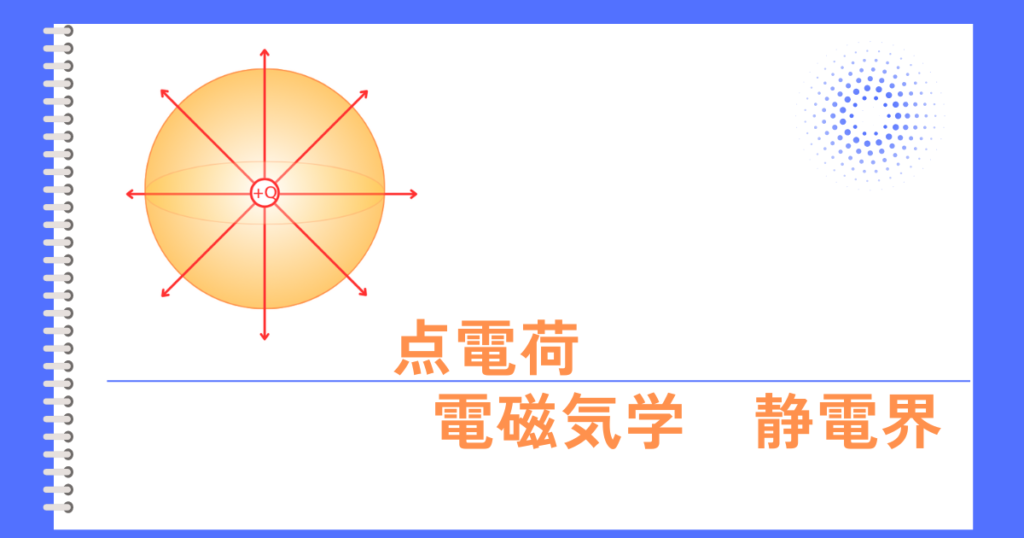
点電荷からの電気力線の広がりは、3次元的に全方面に放射状に広がりますので、閉曲面Sは、球状となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、球の表面積となります。
球の表面積は、\(S=4πr^2\)なので、
\(\displaystyle E=\frac{Q}{ε_0S}\)
→ \(\displaystyle E=\frac{Q}{4πε_0r^2}\)
となります。
線電荷の電界強度E
線電荷の電界強度\(E[V/m]\)は
\(\displaystyle E=\frac{Q}{2πε_0r}\)
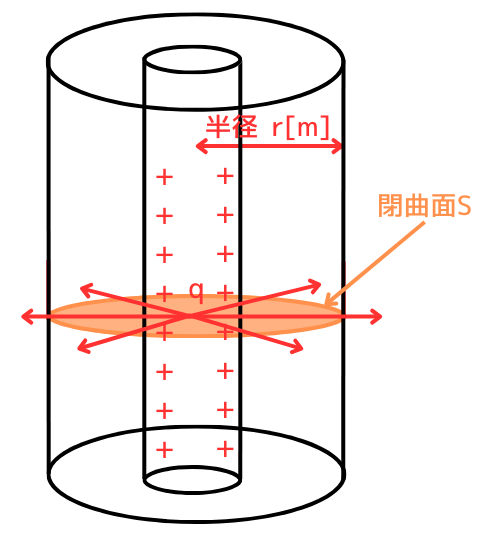
ガウスの法則の式を示します。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
線電荷からの電気力線の広がりは、平面に放射状に広がりますので、閉曲面Sは円周状となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、円周の長さとなります。
円周の長さは、\(S=2πr\)なので、
\(\displaystyle E=\frac{Q}{2πε_0r}\)
となります。
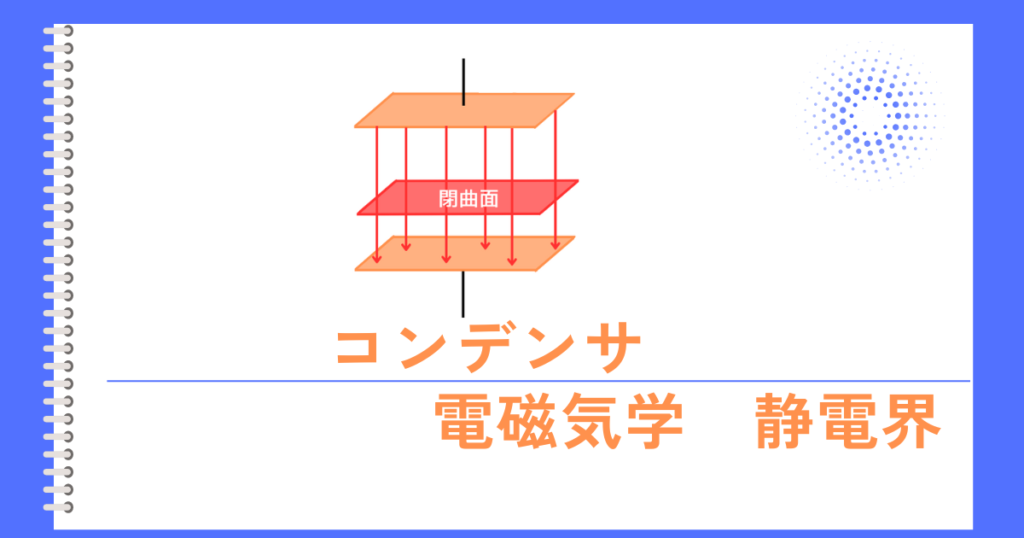
コンデンサの電界強度E
コンデンサの電界強度\(E[V/m]\)は
\(\displaystyle E=\frac{Q}{ε_0S}\)
ガウスの法則の式を示します。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
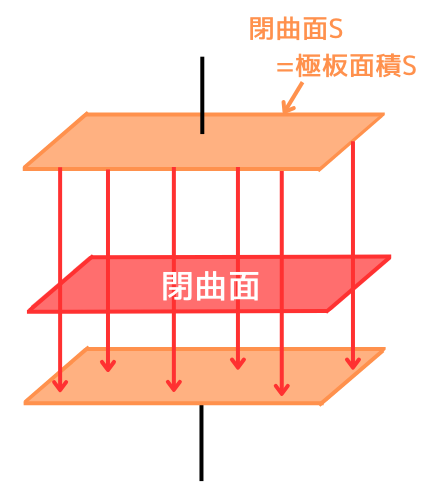
平行平板コンデンサの極板間の電気力線は広がりませんので、閉曲面Sは、極板の表面となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、極板面積Sで一定ですので、
\(\displaystyle E=\frac{Q}{ε_0S}\)
となります。
ガウスの法則と電束密度D
「ガウスの法則と電界強度E」の内容と重複する内容であるため、要点を列挙します。
電界強度\(E[V/m]\)と、電束密度\(D[C/m^2]\)の関係は、
\(D=ε_0E\)
ガウスの法則によって表される電荷Qと電束密度Dの関係の式は、次式となります。
\(\displaystyle \oint_S DdS=Q\)
点電荷の電束密度\(D[C/m^2]\)は
\(\displaystyle D=\frac{Q}{4πr^2}\)
線電荷の電束密度\(D[C/m^2]\)は
\(\displaystyle D=\frac{Q}{2πr}\)
コンデンサの電束密度\(D[C/m^2]\)は
\(\displaystyle D=\frac{Q}{S}\)
何故、電束密度\(D[C/m^2]\)を考える必要があるのか。
それは、誘電体(絶縁体)に電界を与えた時、誘電分極という現象が発生するためです。
誘電分極を加味して考えると、今まで示してきたガウスの法則の式\(\displaystyle \oint_S EdS=\frac{Q}{ε}\)は複雑化し、取り扱いしづらくなります。
そのため、誘電分極の影響を受けずガウスの法則を立式したい場合は、誘電率\(ε\)を式中から無くすために、\(\displaystyle \oint_S DdS=Q\)として立式します。
本記事では、静電界の解説の導線が作りやすいため、電界強度\(E\)を主軸にして説明しています。
また、電験二種・三種では誘電分極について考慮する問題は、ほぼ出題されませんので、誘電分極について深く調べる必要性はないと思われます。
補足
電気力線の本数N
電気力線の本数N[本]は、次式で定義されます。
\(\displaystyle N=\frac{Q}{ε_0}\)
電界強度\(E[V/m]\)は、電気力線の本数\(N\)[本]の密度です。
電気力線の本数を\(\displaystyle N=\frac{Q}{ε_0}\)とすることによって、
ガウスの法則の式を次のように簡略化できます。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
⇒\(\displaystyle \oint_S EdS=N\)
積分の形だとわずらわしいので、
\(\oint_S EdS=ES\)
と展開すると、
\(ES=N\) ⇒ \(\displaystyle E=\frac{N}{S}\)
となります。
このことから、電界強度\(E[V/m]\)は、電気力線の本数\(N\)[本]の密度であると、関係性を導きました。
球の表面積の求め方
半径\(r\)の球の表面積\(4πr^2\)がどのように求まるかを示します。
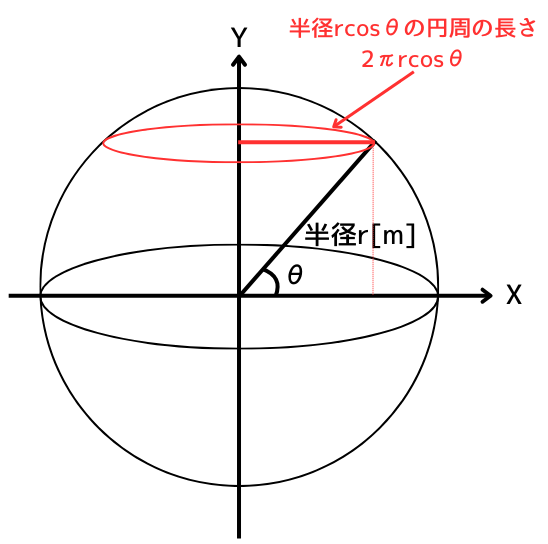
中心からの角度が\(θ\)のときに、Y軸を中心とした円を描きます。
このときの半径は、\(rcosθ\)です。
円周を描くと、その長さは\(2πrcosθ\)となります。
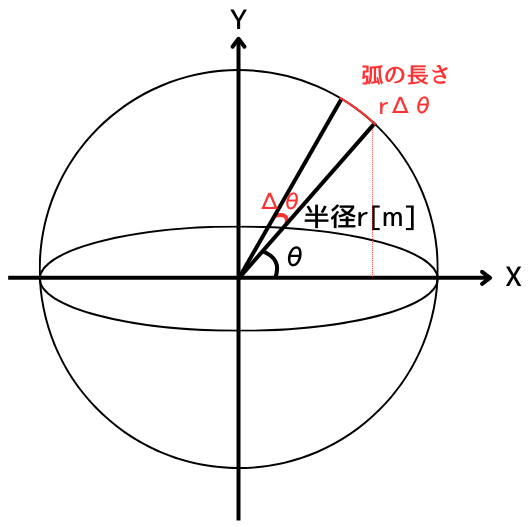
次に、左図のように、中心からの角度を\(Δθ\)だけ動かし、\(θ+Δθ\)に変化させます。
この時の、弧の長さは\(rΔθ\)です。
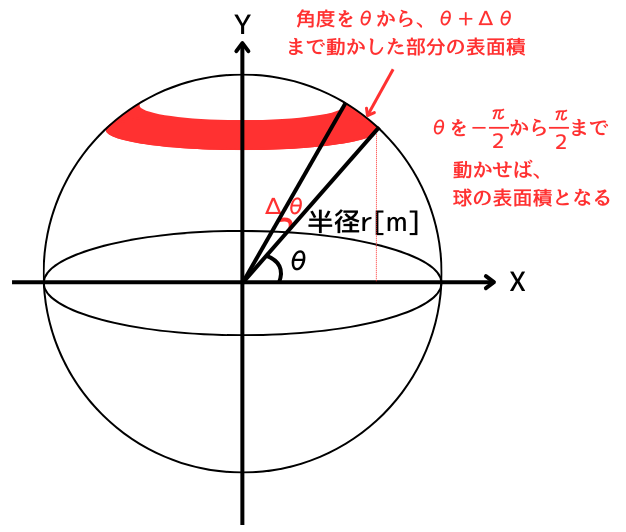
中心からの角度を\(Δθ\)だけ動かした時に描く、左図の赤帯で塗った範囲の表面積\(ΔS\)は、
・円周の長さ \(2πrcosθ\)
・弧の長さ \(rΔθ\)
の積で求められます。
\(ΔS=2πrcosθ・rΔθ=2πr^2cosθΔθ\)
この面積を、\(θ=-\frac{π}{2}\)から、\(θ=\frac{π}{2}\)の範囲の積分を求めれば球の表面積が求まります。
したがって、
\(\displaystyle \begin{eqnarray}
S&=&\int_{-\frac{π}{2}}^\frac{π}{2} 2πr^2cosθdθ = 2πr^2 [sinθ]_{-\frac{π}{2}}^\frac{π}{2} =2πr^2(1-(-1))=4πr^2
\end{eqnarray}\)
以上で、球の表面積\(S=4πr^2\)が求まりました。
余談ですが、球の体積は、球の表面積の式に対して、\(r=0\)から、\(r=r\)の範囲まで積分することで求まります。
\(\displaystyle V=\int_0^r 4πr^2 dr = \frac{4}{3}πr^3\)
過去問
難易度 ★★☆☆☆
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント