概要
静電気力(クーロン力)の基本的な性質と、大きさの計算に関する解説をします。
また、静電気力の計算では、ベクトルの計算も欠かすことができないので、一緒に解説をしていきます。
静電気力(クーロン力)について
一様な電界Eの中で働くクーロン力F[N]
電界\(E[V/m]\)の中に\(q[C]\)に帯電した物体が置かれているとき、物体には力が働きます。この働く力を静電気力(クーロン力)と呼び、その大きさ\(F[N]\)は、次式で表されます。
\(F=qE\)
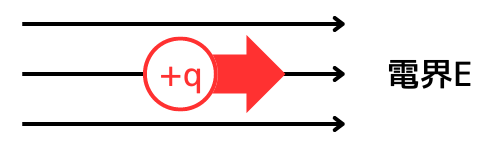
電界\(E\)の中にある正電荷\(q[C]\)には、電界の向きと同じ方向に、静電気力が働きます。
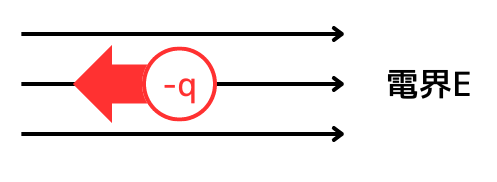
電界\(E\)の中にある負電荷\(-q[C]\)には、電界の向きと逆方向に、静電気力が働きます。
2つの点電荷間に働くクーロン力F[N]
クーロン力の働く向き
・「正電荷-正電荷」「負電荷-負電荷」の符号が同じ時、電荷間に斥力が働きます。
・「正電荷-負電荷」の符号が違う時、電荷間に引力が働きます。
クーロン力の大きさ
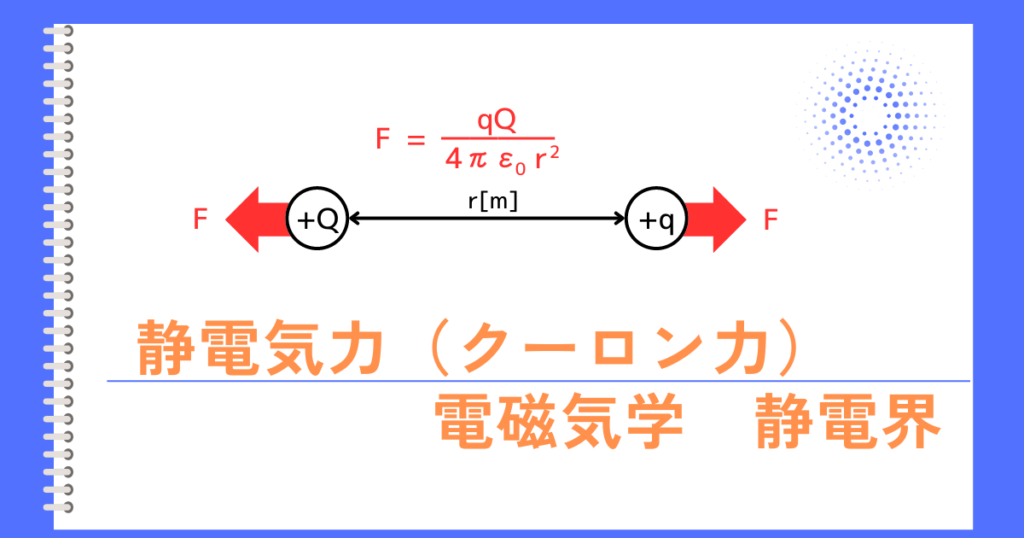
二つの点電荷が\(Q[C]\)、\(q[C]\)としたとき、二つの点電荷には、次の式で示されるクーロン力が働きます。
\(\displaystyle F=\frac{Qq}{4πεr^2}\)
同じ符号の電荷間に斥力が働く理由
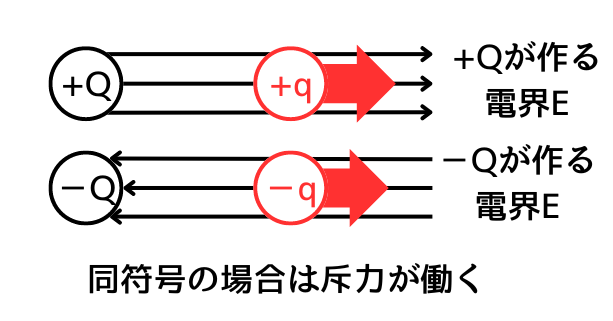
\(+Q\)・\(+q\)の時
\(+Q\)から放出される電界\(E\)と同じ方向に\(+q\)に静電気力が発生するため、斥力となります。
\(-Q\)・\(-q\)の時
\(-Q\)に吸引される電界\(E\)と逆方向に\(-q\)に静電気力が発生するため、斥力となります。
異なる符号の電荷間に引力が働く理由
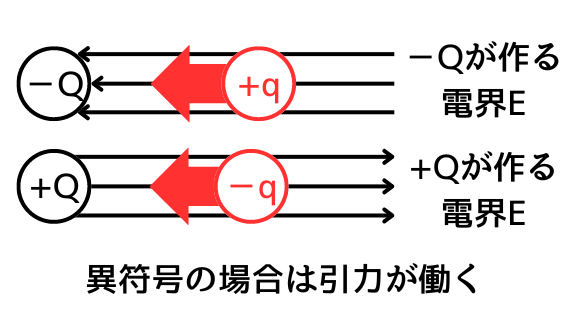
\(-Q\)・\(+q\)の時
\(-Q\)に吸引される電界\(E\)と同じ方向に\(+q\)に静電気力が発生するため、引力となります。
\(+Q\)・\(-q\)の時
\(+Q\)から放出される電界\(E\)と逆方向に\(-q\)に静電気力が発生するため、引力となります。
二つの点電荷に働くクーロン力の大きさ
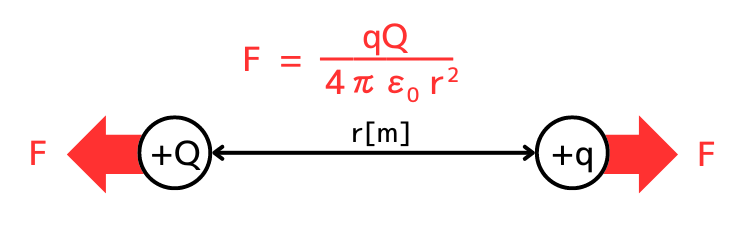
① 点電荷\(q[C]\)に働く静電気力の大きさの導出
点電荷\(Q[C]\)が作り出した電界\(E_Q[V/m]\)内に存在する点電荷\(q[C]\)に働く静電気力\(F[N]\)が\(\displaystyle F=\frac{Qq}{4πεr^2}\)であることを導出します。
点電荷\(Q[C]\)が作り出した電界\(E_Q[V/m]\)の大きさは、ガウスの法則から、
\(\displaystyle \oint_S E_QdS=\frac{Q}{ε_0}\)
→ \(\displaystyle E_Q=\frac{Q}{ε_0S}=\frac{Q}{4πε_0r^2}\)
静電気力の大きさの式は\(F=qE_Q\)なので、電界の大きさを代入すると、
\(\displaystyle F=\frac{qQ}{4πε_0r^2}\)
となります。
② 点電荷\(Q[C]\)に働く静電気力の大きさの導出
①と同じく、点電荷\(q[C]\)が作り出した電界\(E_q[V/m]\)内に存在する点電荷\(Q[C]\)に働く静電気力\(F[N]\)が\(\displaystyle F=\frac{Qq}{4πεr^2}\)であることを導出します。
点電荷\(q[C]\)が作り出した電界\(E_q[V/m]\)の大きさは、ガウスの法則から、
\(\displaystyle E_q=\frac{q}{4πε_0r^2}\)
静電気力の大きさの式は\(F=QE_q\)なので、電界の大きさを代入すると、
\(\displaystyle F=\frac{qQ}{4πε_0r^2}\)
となります。
以上、①・②から、\(+Q\)・\(+q\)のどちらの電荷にも、同じ大きさの静電気力\(\displaystyle F=\frac{qQ}{4πε_0r^2}\)が働く事を示しました。
クーロン力の合成
クーロン力を求める問題は、複数の電荷が点在していて、違う方向を向くベクトルの和を求める様な形式の出題が多いです。そのため、クーロン力とベクトルの合成はワンセットで学習しましょう。
ベクトルの合成
同方向のベクトルの合成
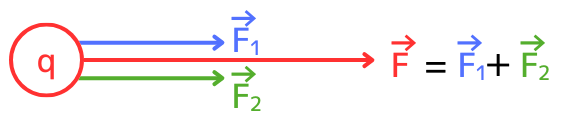
左図のように、同じ方向を向いている力のベクトルが2つあるときのベクトル合成をします。
\(\vec{F_1}\)と、\(\vec{F_2}\)の2つのベクトルがあるとしたとき、合成したベクトルを\(F\)とすると、合成ベクトルの式は、
\(\vec{F}=\vec{F_1}+\vec{F2}\) です。
そして、合成ベクトルの大きさは
\(F=F_1+F_2\)
となります。
方向が違うベクトルの合成
2つのベクトル\(F_1\)と\(F_2\)があり、それぞれの間に\(θ\)の角度があったとします。
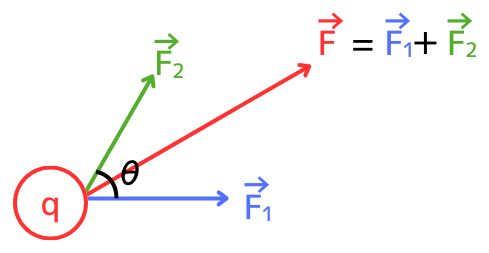
この2つを合成したベクトルを\(F\)とすると、
\(\vec{F}=\vec{F_1}+\vec{F2}\)
です。
次に、ベクトルの大きさを求めます。
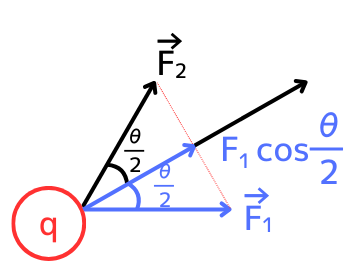
\(\vec{F_1}\)が、\(\vec{F}\)と同じ向きに作るベクトルの大きさは、\(F_1cos\frac{θ}{2}\)です。
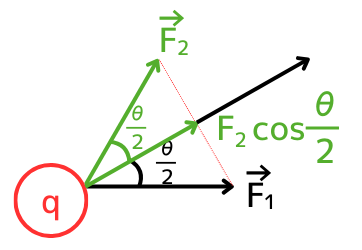
\(\vec{F_2}\)が、\(\vec{F}\)と同じ向きに作るベクトルの大きさは、\(F_2cos\frac{θ}{2}\)です。
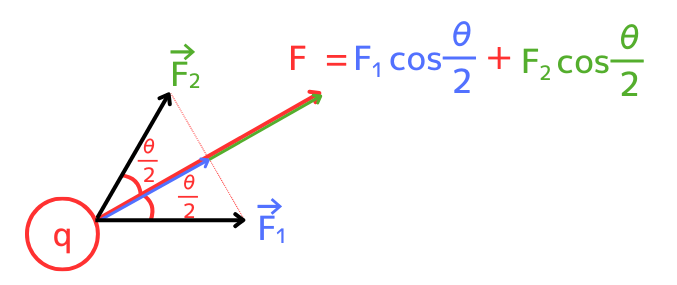
これらを合成すると、\(\vec{F}\)の大きさ\(F\)は、
\(F=F_1cos\frac{θ}{2}+F_2cos\frac{θ}{2}\)
です。
補足
静電気力と重力の比較
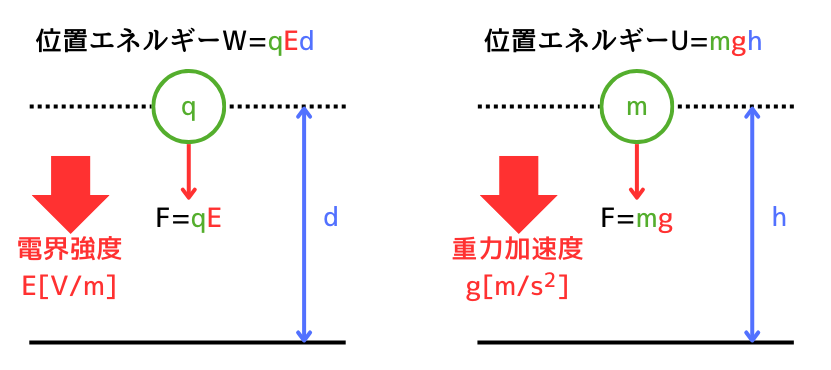
電界の中に帯電した物体がある時、その物体には静電気力\(F=qE\)が働きます。
この静電気力\(F\)は、重力\(F=mg\)と比較すると同じような式であることがわかります。
これは、静電気力による位置エネルギー(ポテンシャルエネルギー)と、物質の高さによる位置エネルギーと比較しても同様であることがわかります。
| 一様な電界 | 重力 | |
| 力 | \(F=qE\) | \(F=mg\) |
| 位置エネルギー | \(W=qEd\) | \(U=mgh\) |
過去問
難易度 ★☆☆☆☆
電験三種 令和3年度 問2
難易度 ★★☆☆☆
電験三種 令和4年度上期 問2
難易度 ★★★☆☆
電験三種 令和5年度下期 問12
難易度 ★★★★☆
電験三種 令和5年度下期 問2
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント