概要
点電荷が作り出す電界中の2点間の電位差について求める問題です。
電位に関する式を理解していれば容易に回答できます。
キーワード
電位、電位差
問題
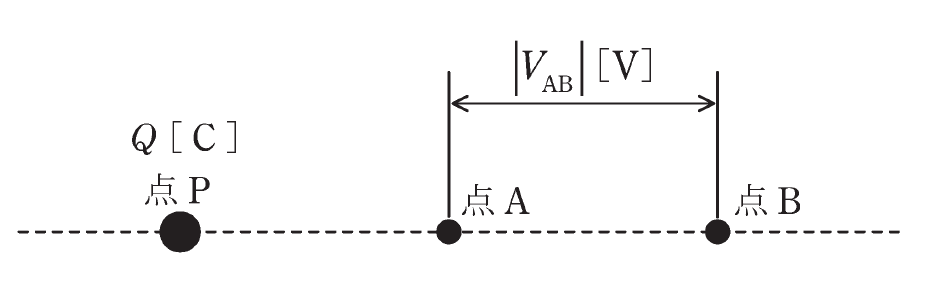
図のように、真空中に点P、点A、点Bが直線状に配置されている。
点Pは\(Q[C]\)の点電荷を置いた点とし、A-B間に生じる電位差の絶対値を\(|V_{AB}|[V]\)とする。
次の(a)~(d)の四つの実験を個別に行ったとき、\(|V_{AB}|[V]\)の値が最小となるものと最大になるものの実験の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
[実験内容]
(a)P-A間の距離を2m、A-B間の距離を1mとした。
(b)P-A間の距離を1m、A-B間の距離を2mとした。
(c)P-A間の距離を0.5m、A-B間の距離を1mとした。
(d)P-A間の距離を1m、A-B間の距離を0.5mとした。
(1)(a)と(b) (2)(a)と(c) (3)(a)と(d)
(4)(b)と(c) (5)(c)と(d)
答え
(2)
要点整理
電位V[V]
点電荷\(Q[C]\)が作り出す電界\(E[V/m]\)の場における電位\(V[V]\)は、誘電率\(ε[F/m]\)、距離\(r[m]\)を使用して次式で表されます。
\(\displaystyle V=\frac{Q}{4πεr}\)
電位の式を導出します。
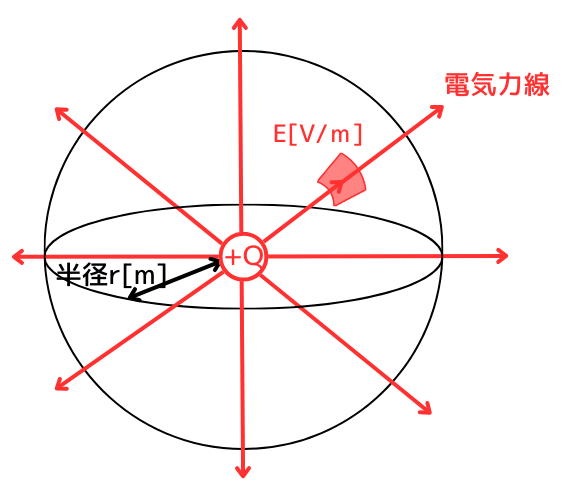
点電荷\(Q[C]\)から、\(N\)本の電気力線が放射状に出ます。
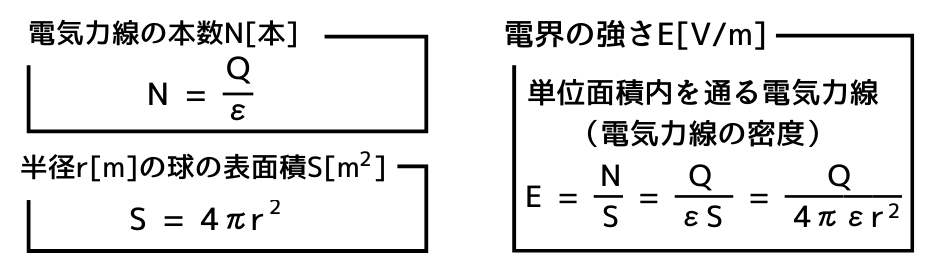
電気力線の本数\(N\)[本]は、次の①式で表されます。
\(\displaystyle N=\frac{Q}{ε}\)[本] ………①
電界強度\(E[V/m]\)は、電気力線の本数の密度と等しいです。そのため、点電荷\(Q[C]\)から距離\(r[m]\)の点の球の表面積を\(S[m^2]\)とすると、電界強度は次式で表されます。
\(\displaystyle E=\frac{N}{S}[V/m]\) ………②
半径\(r[m]\)の球の表面積\(S[m^2]\)は、
\(S=4πr^2[m^2]\) ………③
①・③式を②式に代入すると、
\(\displaystyle E=\frac{Q}{4πεr^2}[V/m]\) ………④
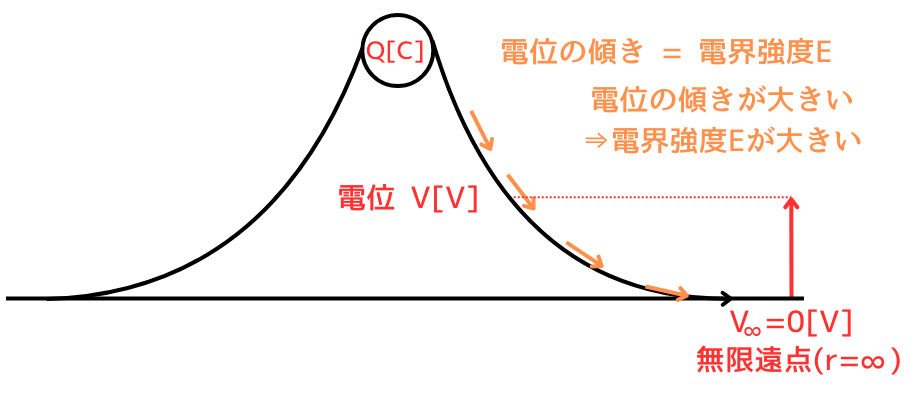
電界強度\(E[V/m]\)は、電位\(V[V]\)傾きです。これを式に表すと、
\(\displaystyle E=-\frac{dV}{dr}\) ………⑤
※電位\(V\)は電界から受けるクーロン力に逆らって電荷が動いた時に大きくなるので、マイナスが付きます。
⑤式の両辺を距離rに対して積分すると、電位\(V\)の式となります。
\(V=-\int_{基点}^{対象点}E dr\) ………⑥
※基点が定義されていないとき、つまり、単純に電位\(V[V]\)を求めるようなときは、
無限遠点:\(\infty\) を基点とします。
⑥式に④を代入して積分します。
この時、基点を無限遠点(\(\infty\))、対象点を\(r[m]\)離れた点とします。
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{\infty}^{r} \frac{Q}{4πεr^2} dr
&=&\frac{Q}{4πε} \left[ r \right]_{\infty}^{r} = \frac{Q}{4πεr}
\end{eqnarray}\)
以上より、\(\displaystyle V=\frac{Q}{4πεr}\) が導出出来ました。
補足
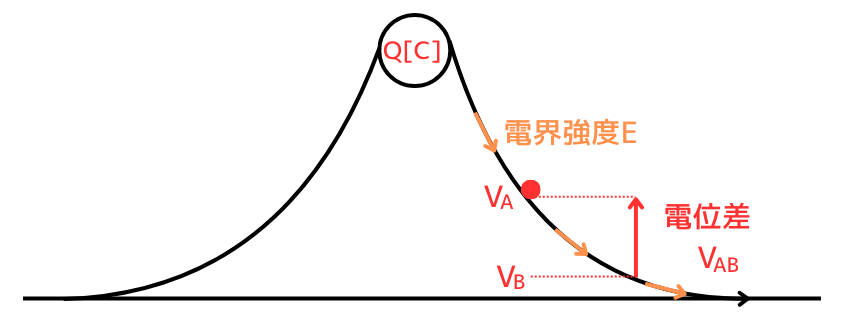
基点を無限遠点\(\infty\)としなかった場合の電位差\(V_{AB}\)を求めてみます。
\(Q[C]\)の電荷からの距離が\(r_B[m]\)である点B(基点)から、距離\(r_A[m]\)である点A(対象点)までの電位差を\(V_{AB}[V]\)としたとき、次の通り計算できます。
\(\displaystyle \begin{eqnarray}
V_{AB}&=& -\int_{r_B}^{r_A} \frac{Q}{4πεr^2} dr = \frac{Q}{4πε} \left[ \frac{1}{r} \right]_{r_B}^{r_A} \\
&=&\frac{Q}{4πεr_A}-\frac{Q}{4πεr_B} = V_A-V_B
\end{eqnarray}\)
回答解説
\(Q[C]\)の電荷から\(r[m]\)離れた点の電位の式は、次式で表されます。
\(\displaystyle V=\frac{Q}{4πε_0r}\) ………①
この①式に、距離を代入することで、(a)~(d)の各条件における点A、点Bの電位\(V_A[V]\)、\(V_B[V]\)と、点Aと点Bの電位差の絶対値\(|V_{AB}|[V]\)を求めます。
なお、\(|V_{AB}|=|V_A-V_B|\)です。
| 点Aの電位 \(V_A[V]\) | 点Bの電位 \(V_B[V]\) | 点Aと点Bの電位差 \(|V_{AB}|[V]\) | |
| (a) | \(\displaystyle \frac{Q}{8πε_0}\) | \(\displaystyle \frac{Q}{12πε_0}\) | \(\displaystyle \frac{Q}{24πε_0}\) |
| (b) | \(\displaystyle \frac{Q}{4πε_0}\) | \(\displaystyle \frac{Q}{12πε_0}\) | \(\displaystyle \frac{Q}{6πε_0}\) |
| (c) | \(\displaystyle \frac{Q}{2πε_0}\) | \(\displaystyle \frac{Q}{6πε_0}\) | \(\displaystyle \frac{Q}{3πε_0}\) |
| (d) | \(\displaystyle \frac{Q}{4πε_0}\) | \(\displaystyle \frac{Q}{6πε_0}\) | \(\displaystyle \frac{Q}{12πε_0}\) |
上の表より、\(|V_{AB}|[V]\)の値が最小になるものは(a)、最大になるものは(c)であることがわかります。
以上より、答えは (2) です。
出典元
令和元年度第三種電気主任技術者試験 理論科目A問題問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント