難易度
電気計測における誤差率の問題です。計測に関する問題として誤差率の定義について覚えておく必要がありますが、問題としては簡単な部類です。
(a)は非常に簡単です。
(b)は誤差と誤差率の定義についてしっかり理解しておく必要があります。
問題
図のように、電源\(E[V]\)、負荷抵抗\(R[Ω]\)、内部抵抗\(R_v[kΩ]\)の電圧計及び内部抵抗\(R_a[Ω]\)の電流計を接続した回路がある。この回路において、電圧計及び電流計の指示値がそれぞれ\(V_1[V]\)、\(I_1[A]\)であるとき、次の(a)及び(b)の問に答えよ。
ただし、電圧計と電流計の指示値の積を負荷抵抗\(R[Ω]\)の消費電力の測定値とする。
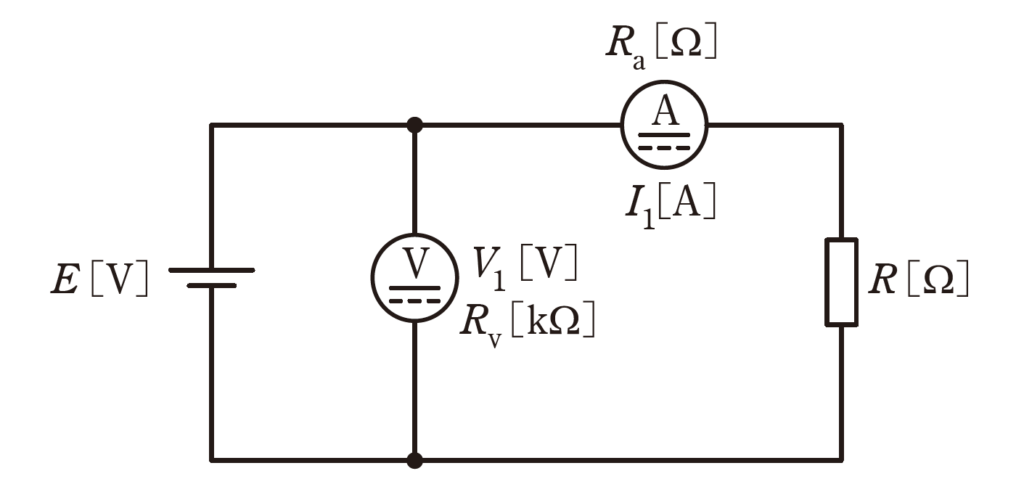
(a) 電流計の電力損失の値\([W]\)を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1)\(\displaystyle \frac{V_1^2}{R_a}\)
(2)\(\displaystyle \frac{V_1^2}{R_a}-I_1^2R_a\)
(3)\(\displaystyle \frac{V_1^2}{R_v}+I_1^2R_a\)
(4)\(I_1^2R_a\)
(5)\(I_1^2R_a-I_1^2R_v\)
(b) 今、負荷抵抗\(R=320Ω\)、電流計の内部抵抗\(R_a=4Ω\)が分かっている。
この回路で得られた負荷抵抗\(R[Ω]\)の消費電力の測定値\(V_1I_1[W]\)に対して、\(R[Ω]\)の消費電力を真値とするとき、誤差率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.3 (2) 0.8 (3) 0.9 (4) 1.0 (5) 1.2
答え
(a) (4)
(b) (5)
要点整理
消費電力P=VIとなる理由
本問を解く上で重要ではないですが、\(P=VI\)となる理由について考えたことはありますか。
余談のような内容ですが、この項目では、消費電力\(P[W]\)が電圧\(V[V]\)と電流\(I[A]\)の積の式
\(P[W]=VI[V・A]\) ………①
として、成り立つ理由について、証明します。
消費電力\(P[W]\)は、仕事率です。仕事率とは、時間当たりの仕事\(W[J]\)なので、
\(\displaystyle P[W]=\frac{W}{t}[J/s]\) ………②
です。
仕事\(W[J]\)は、力\(F[N]\)を加えて距離\(d[m]\)動かした時の積なので、
\(W[J]=Fd[Nm]\) ………③
です。
クーロン力\(F[N]\)は、電荷\(q[C]\)と、電界の強さ\(E[V/m]\)の積なので、
\(F[N]=qE[CV/m]\) ………④
電流\(I[A]\)は、電荷\(1[C]\)が1秒間\([/s]\)に移動したときに\(1[A]\)なので、
\(\displaystyle I[A]=\frac{q}{t}[C/s]\)
⇔\(q[C]=It[As]\) ………⑤
電位\(V[V]\)と、電界の強さ\(E[V/m]\)の関係は、単位からもわかる通り、
\(V[V]=E・d[V/m・m]\) ………⑥
です。
証明のための材料がそろったので、①式を証明していきます。
②式から、式を展開していきます。
\(\displaystyle \begin{eqnarray}
P&=&\frac{W}{t} ③式を代入 \\ \\
&=&\frac{Fd}{t} ④式を代入\\ \\
&=&\frac{qEd}{t} ⑤式を代入\\ \\
&=&IEd ⑥式を代入\\
&=&IV
\end{eqnarray}\)
以上より、①式の\(P[W]=VI[V・A]\)が証明出来ました。
誤差率
電圧計、電流計には、内部抵抗による測定誤差が必ず発生します。
その誤差を評価するために、真値、測定値、誤差、誤差率があります。
測定値\(M\)は、電圧計、電流計が指し示す数値です。\(M\)は、\(Measure\)の頭文字です。
真値\(T\)は、誤差の無い正しい数値です。\(T\)は、\(True\)の頭文字です。
誤差\(ε\)は、測定値と真値の差で、\(ε=M-T\)で表されます。
誤差率\(ε_{\%}\)は、誤差\(ε\)を真値\(T\)で割ることで率表示にしたものです。
\(\displaystyle ε_{\%}=\frac{ε}{T}×100[\%]=\frac{M-T}{T}×100[\%]\)
【余談】
誤差率\(ε_{\%}\)の分母が測定値\(M\)か、真値\(T\)かで悩むこともあると思います。
測定値\(M\)を分母にしてしまうと、使用している計器の精度によって誤差率がぶれてしまいます。
そのため、真値\(T\)を分母にしなければ正しく評価することは出来ないと理解しましょう。
回答解説
問(a)
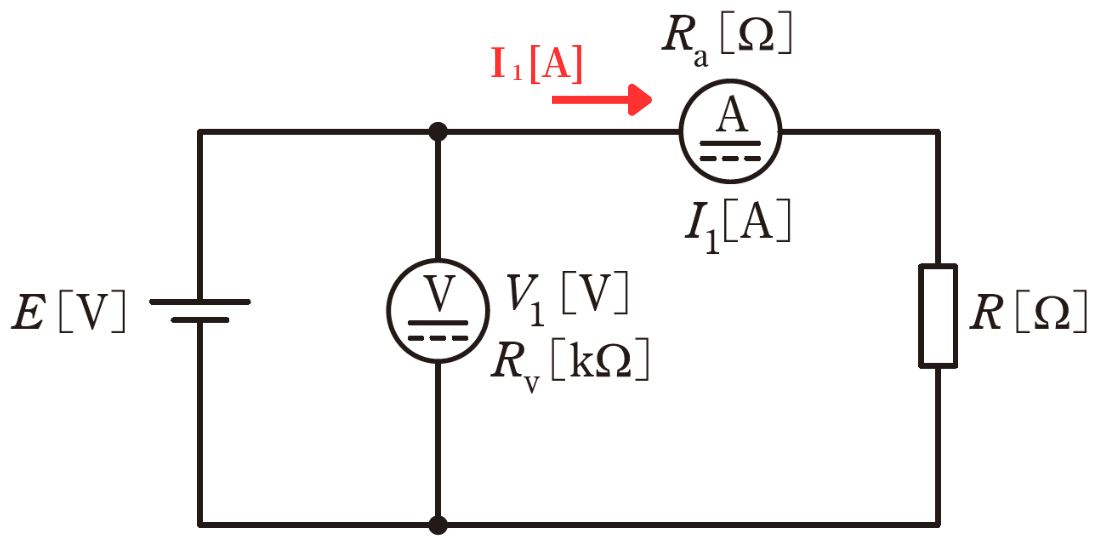
電流計の測定値が\(I_1[A]\)なので、電流計の内部抵抗\(R_a[Ω]\)で消費される消費電力\(P_a\)は、
\(P_a=I_1^2R_a[W]\)
です。
したがって、(4)\(P_a=I_1^2R_a[W]\)が答えです。
問(b)
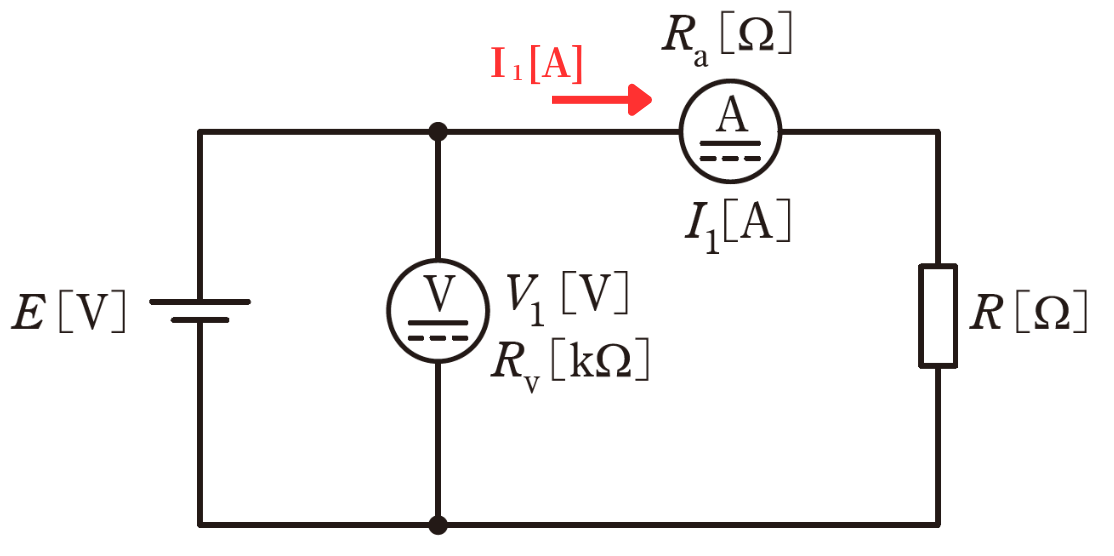
抵抗\(R[Ω]\)に流れる電流\(I_1[A]\)は、
\(\displaystyle \begin{eqnarray}
I_1&=&\frac{E}{R_a+R}=\frac{E}{4+320}\\ \\
&=&\frac{E}{324}[A] ………①
\end{eqnarray}\)
消費電力の真値\(P_T\)は、\(P_T=I_1^2R\) ………②
消費電力の測定値\(P_M\)は、\(P_M=V_1I_1=EI_1\) ………③
誤差率\(ε_{\%}\)は、
\(\displaystyle \begin{eqnarray}
ε_{\%}&=&\frac{P_M-P_T}{P_T}×100=\frac{EI_1-I_1^2R}{I_1^2R}×100\\
&=&\frac{E-I_1R}{I_1R}×100=\frac{E-\frac{320}{324}E}{\frac{320}{324}E}×100=1.25[\%]
\end{eqnarray}\)
したがって、(5)1.2 が答えです。
出典元
令和5年度第三種電気主任技術者試験 理論科目B問題下期問16
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント