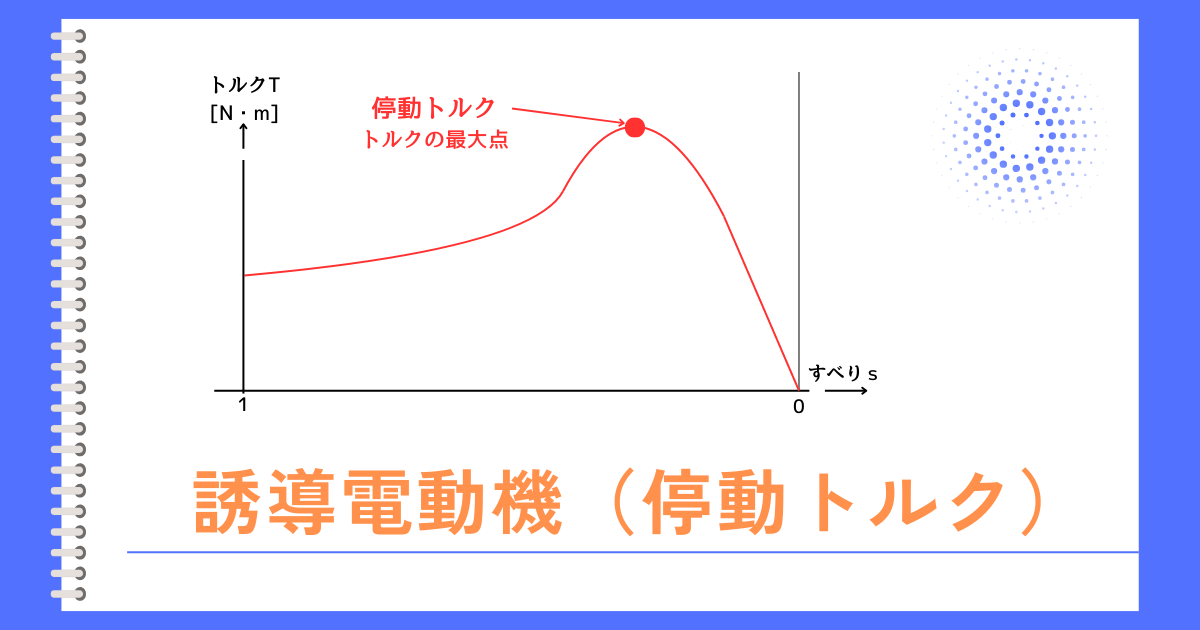
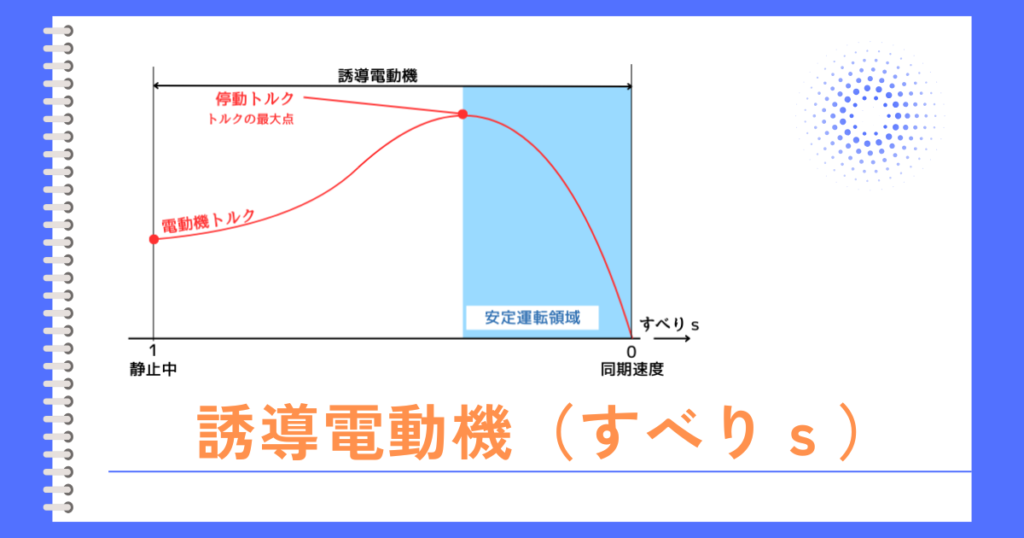
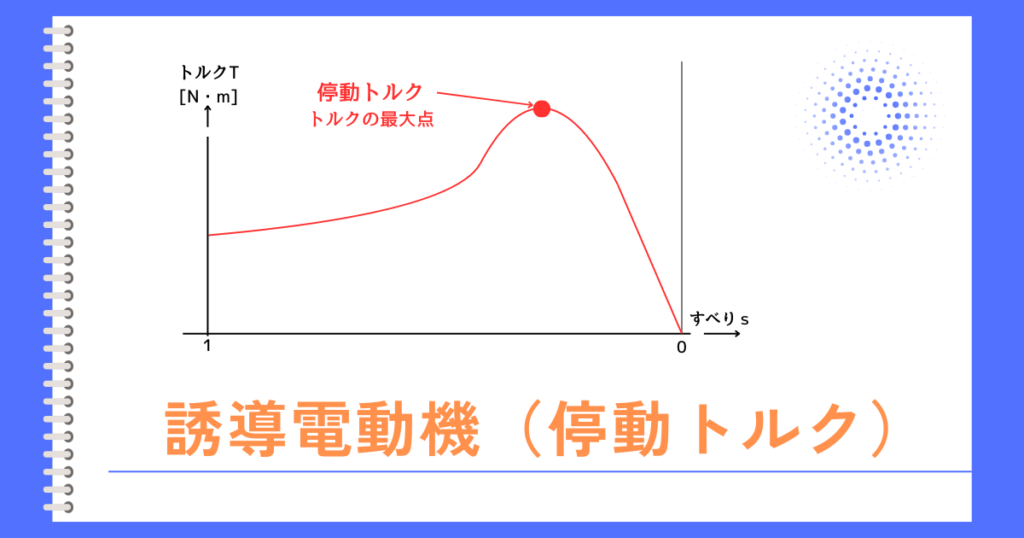
停動トルクとは
停動トルクとは、誘導電動機が出力できる最大トルク(回転力)の事です。
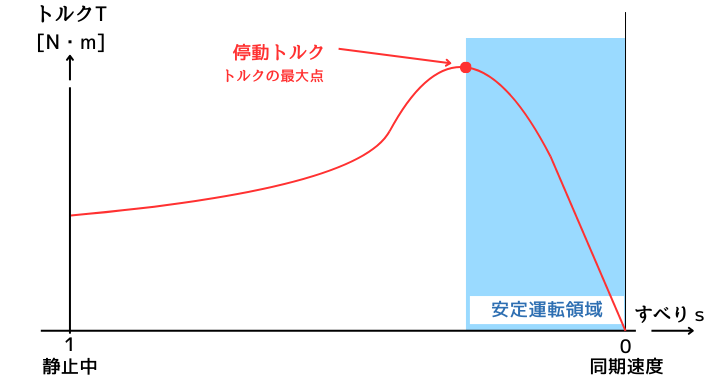
停動トルク(最大トルク)を上回る過負荷がかかったとき、負荷に対して電動機の回転力が不足します。
その結果、誘導電動機は最終的に動作を停止(停動)してしまいます。そのことから、停動トルクと呼ばれます。
誘導電動機が過負荷で停止してしまうと、始動電流が流れ続けてしまいます。
始動電流は定格電流よりも数倍大きな電流であることから、誘導電動機の異常過熱による焼損につながるため、停動トルクは重要な要素です。
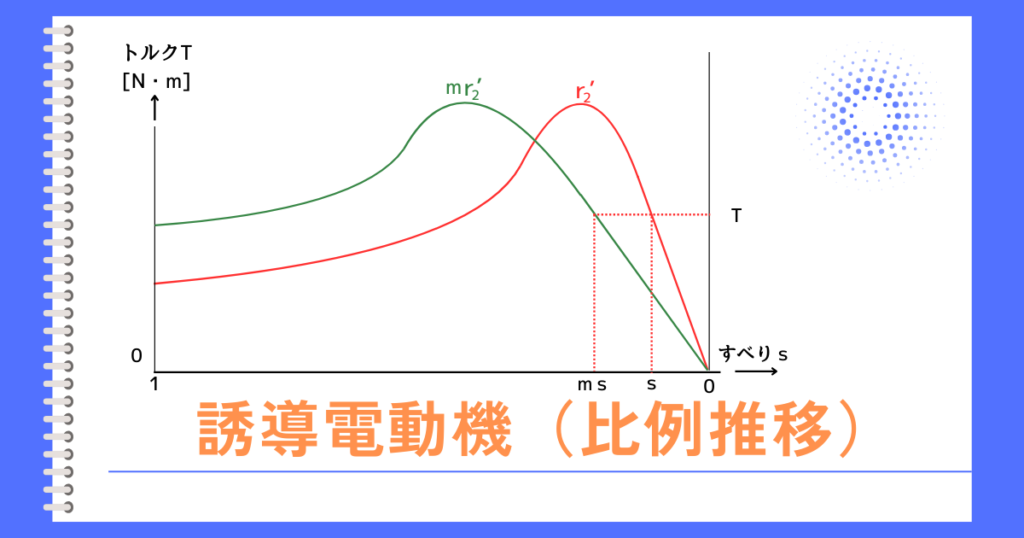
停動トルクは、二次抵抗\(r’_2\)に影響を受けないという特徴があります。
そのため、巻線形誘導機で比例推移のために外部抵抗を変化させても、停動トルクは維持したまますべりートルク特性のグラフは変化します。
停動トルクと負荷
誘導電動機の運転中に、負荷が変動することがあります。
その負荷の変動によって、停動トルク以下の負荷の場合と、停動トルク以上の負荷の場合に分けて、すべりとトルクがどのように変動するかを図示していきます。
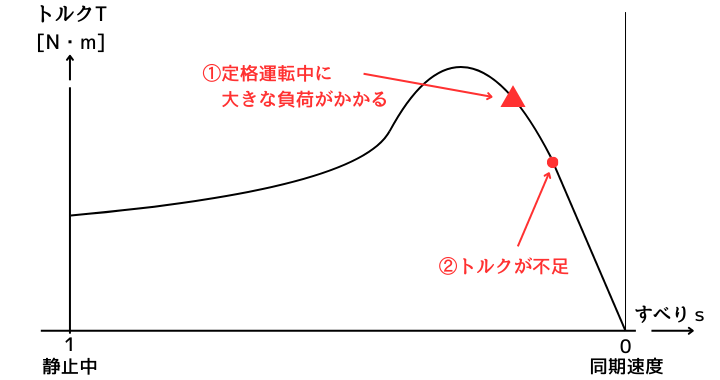
停動トルク以下の負荷がかかった場合のすべりの変化
➡

誘導電動機が運転している最中に大きな負荷がかかると、トルクが不足するため減速していきます。(すべりは増加)
減速していくと、停動トルクに至るまでは直線的にトルクが増加していきます。
負荷が停動トルクよりも小さな場合は、負荷と出力トルクが釣り合うすべり\(s\)の点で安定します。
過負荷(停動トルク以上の負荷)がかかった場合のすべりの変化
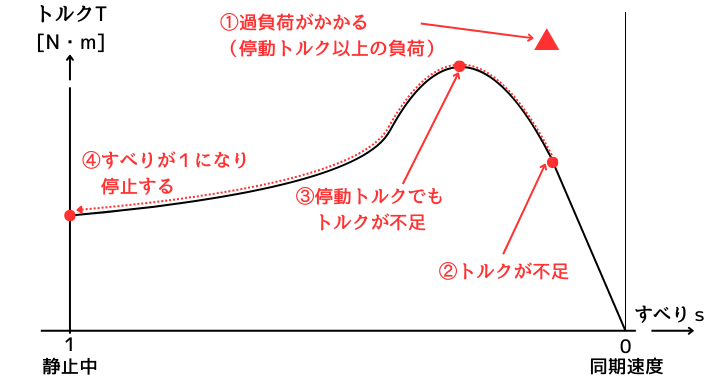
過負荷がかかると、トルクが不足して減速していきます。
減速していくと電動機の出力トルクは上昇していきますが、停動トルクでも過負荷を回転させることはできません。
そのため、さらに減速していき、最終的に停止状態になります。(\(s=1\))
停動トルクの式の導出
停動トルクを出力するときのすべり\(s\)と、トルクの大きさは式で表すことが出来ます。
電験三種では、停動トルクを求めるような問題が出題されることは無いと思いますので、参考程度に、どのように表されるかを計算していきます。
停動トルク時のすべり\(s\)
誘導電動機のトルクは、次式で表されます。
\(\displaystyle T=\frac{3\frac{r’_2}{s}}{\left( r_1+\frac{r’_2}{s} \right)^2+x^2}・\frac{V^2}{ω_s}\) …①
分母が最小のとき、トルク\(T\)は最大値になります。
分母をすべり\(s\)で微分すると、分母が最小となるときのすべり\(s\)がわかります。
\(\displaystyle \frac{d}{ds} s\left( (r_1+\frac{r’_2}{s} )^2+x^2\right) =0 \)
⇔ \(\displaystyle \frac{d}{ds} \left(sr^2_1+2r_1r’_2+\frac{r’^2_2}{s}+sx^2 \right)=0 \)
⇔ \(\displaystyle (r^2_1+x^2)-\left( \frac{r’^2_2}{s^2} \right)=0 \)
⇔ \(\displaystyle s=\frac{r’_2}{\sqrt{r^2_1+x^2}}\) …②
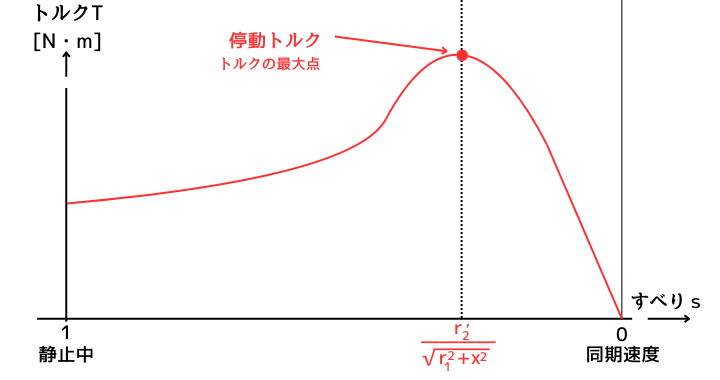
停動トルクの大きさ
誘導電動機のトルク\(T\)の①式に、すべり\(s\)の②式を代入することで計算できます。
まずは、①式を展開していきます。
\(\displaystyle T=\frac{3\frac{r’_2}{s}}{\left( r_1+\frac{r’_2}{s} \right)^2+x^2}・\frac{V^2}{ω_s}=\frac{3r’_2}{sr^2_1+2r_1r’_2+\frac{r’^2_2}{s}+sx^2}・\frac{V^2}{ω_s}\) …③
計算の簡略化のため、③式の分母だけを取り出して②式を代入します。
\(\begin{eqnarray}
分母&=&sr^2_1+2r_1r’_2+\frac{r’^2_2}{s}+sx^2 \\ \\
&=&\frac{r’_2(r^2_1+x^2)}{\sqrt{r^2_1+x^2}}+2r_1r’_2+\frac{\sqrt{r^2_1+x^2}}{r’_2}r’^2_2 \\ \\
&=&r’_2\sqrt{r^2_1+x^2}+2r_1r’_2+r’_2\sqrt{r^2_1+x^2} \\ \\
&=&2r’_2\sqrt{r^2_1+x^2}+2r_1r’_2 \\ \\
&=&2r’_2(r_1+\sqrt{r^2_1+x^2}) …④
\end{eqnarray}\)
④式を③式に代入します。
\(\displaystyle \begin{eqnarray}
T&=&\frac{3r’_2}{sr^2_1+2r_1r’_2+\frac{r’_2}{s}+sx^2}・\frac{V^2}{ω_s} \\ \\
&=&\frac{3r’_2}{2r’_2(r_1+\sqrt{r^2_1+x^2})}・\frac{V^2}{ω_s} \\ \\
&=&\frac{3}{2}・\frac{1}{r_1+\sqrt{r^2_1+x^2}}・\frac{V^2}{ω_s} …⑤
\end{eqnarray}\)
⑤式から、トルク\(T\)が二次抵抗\(r’_2\)に関係しないことがわかりました。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。







コメント