L形等価回路の計算式

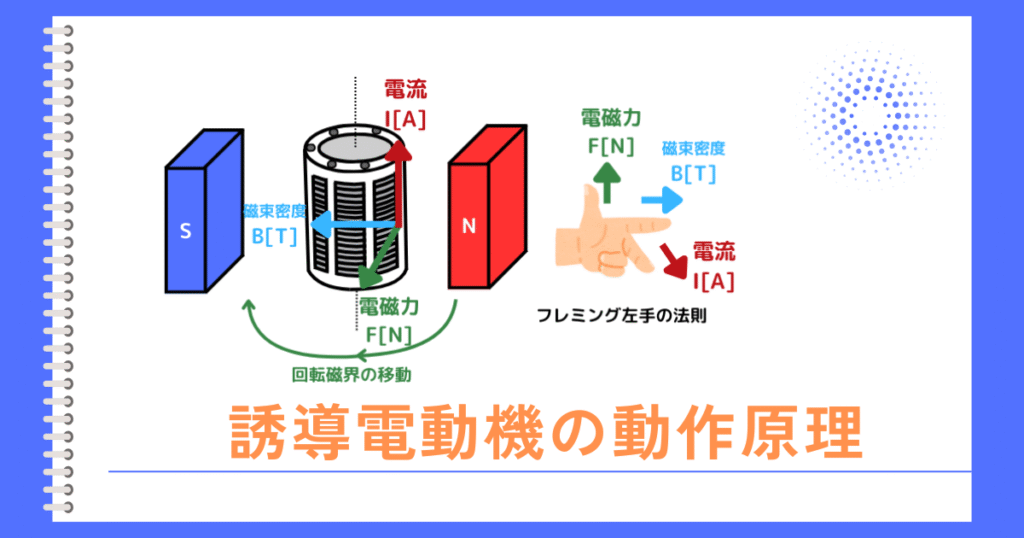
概要

誘導電動機のL形等価回路の計算についてまとめました。

誘導電動機の等価回路図は、一見すると複雑な回路な上、計算も複雑に見えます。
しかし、各要素について一つ一つ理解していけば、電験の中でも得点源にしやすい単元ですので、覚えるのではなく、意味を理解していく事を意識しましょう。

　

誘導電動機の式一覧

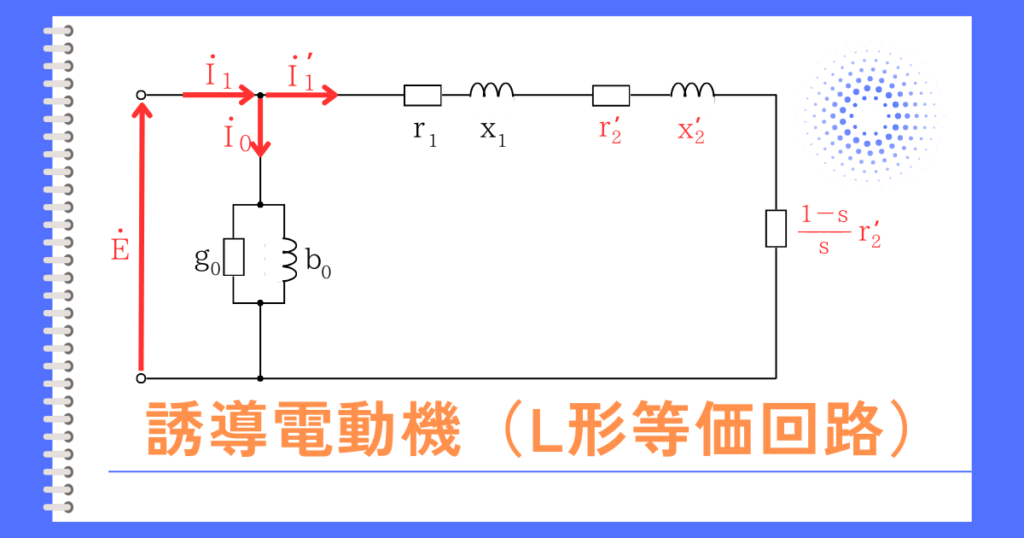
誘導電動機のL形等価回路です。
この回路が、どのように成り立っているかについて理解したうえで、本頁の式を見ていくと理解が深まると思います。　➡　等価回路の成り立ちの解説

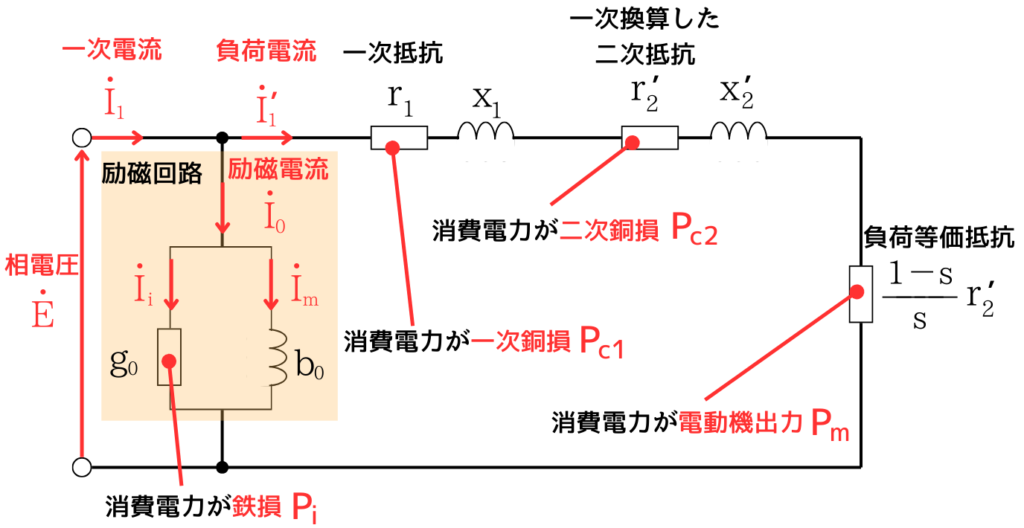
L形等価回路から立式できる式

複雑な式を暗記する価値は無いです。
L形等価回路から、オームの法則を使って立式できるようになりましょう。

次に示す損失・出力に関する式は、一相分の式です。
誘導電動機全体の損失・出力電力を計算する場合は、三相分の電力について考えなければならないので、３倍する必要があります。

負荷電流の大きさ\(I’_1\)
\(\displaystyle I’_1=\frac{E}{\sqrt{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}}\)

二次入力\(P_2\)
\(\displaystyle P_2=3I’^2_1・\frac{r’_2}{s}=\frac{3E^2}{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}・\frac{r’_2}{s}\)

二次銅損\(P_{c2}\)
\(\displaystyle P_{c2}=3I’^2_1・r’_2=\frac{3E^2}{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}・r’_2\)

機械的出力\(P_m\)
\(\displaystyle P_m=3I’^2_1・\frac{1-s}{s}r’_2=\frac{3E^2}{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}・\frac{1-s}{s}r’_2\)

鉄損\(P_i\)
\(P_i=3g_oE^2\)

　

入出力電力と損失の関係式

誘導機の全ての入出力電力と、電力損失の関係は、下図でまとめて表すことが出来ます。

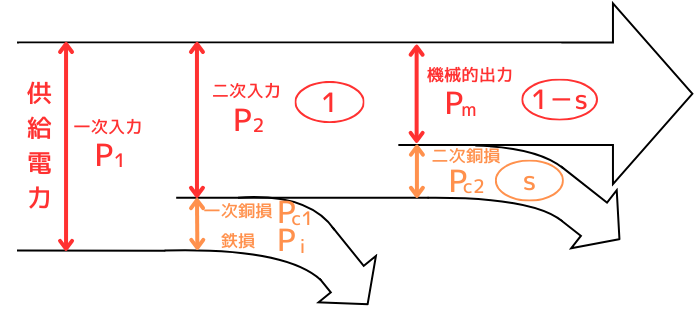
導出は簡単ですが、誘導機の計算をする上で、比較的使う機会が多い関係式です。

二次入力\(P_2\)・二次銅損\(P_{c2}\)・機械的出力\(P_m\)の関係①
\(P_2=P_{c2}+P_m\)

二次入力\(P_2\)・二次銅損\(P_{c2}\)・機械的出力\(P_m\)の関係②
\(P_2:P_{c2}:P_m=1:s:(1-s)\)

一次入力\(P_1\)・機械的出力\(P_m\)・損失\(P_i+P_{c1}+P_{c2}\)の関係
\(P_1=P_m+P_i+P_{c1}+P_{c2}\)

効率\(η\)
\(\displaystyle η=\frac{P_m}{P_i}=\frac{P_m}{P_m+P_i+P_{c1}+P_{c2}}\)

　

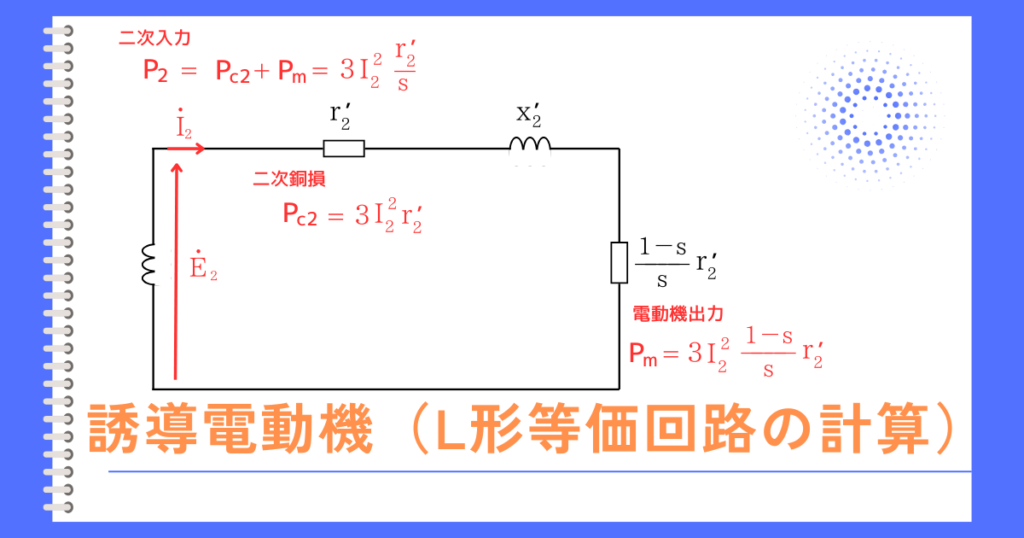
\(P_2:P_{c2}:P_m=1:s:(1-s)\)の導出

二次入力（回転子入力）\(P_2\)、二次銅損\(P_{c2}\)、機械的出力\(P_m\)としたとき、
これらの関係式である\(P_2:P_{c2}:P_m=1:s:(1-s)\)は、三相誘導電動機の計算において頻繁に使います。
理解してこの関係式を使えるようになるために、導出方法を示します。

二次側の等価回路図から、導出します。

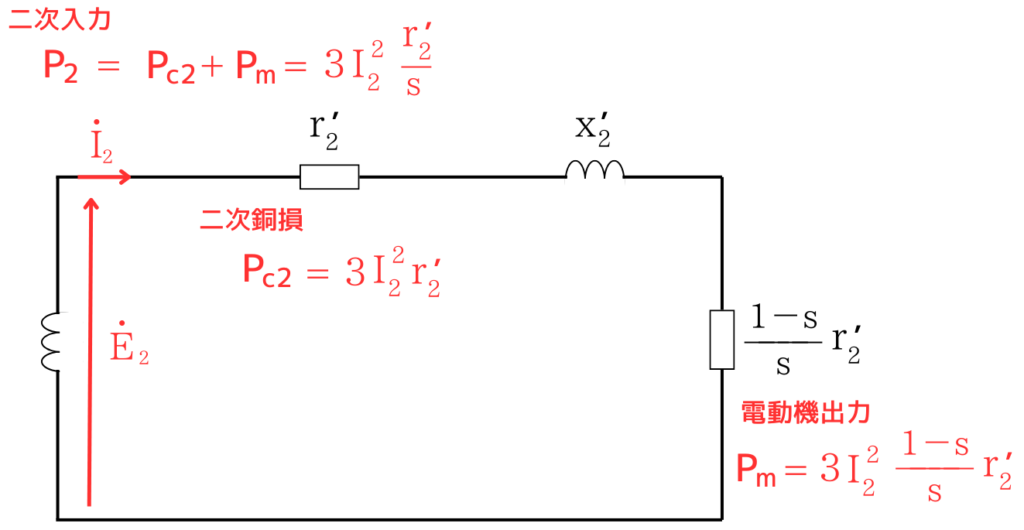
二次入力\(P_2=\)\(\displaystyle P_{c2}+P_m=3I^2_2r’_2+3I^2_2\frac{1-s}{s}r’_2=\)\(\displaystyle 3I^2_2\frac{r’_2}{s}\)

二次銅損\(\displaystyle P_{c2}=3I^2_2r’_2\)

機械的出力二次入力\(\displaystyle P_m=3I^2_2\frac{1-s}{s}r’_2\)

以上をまとめていきますと、
\(\begin{eqnarray}
P_2:P_{c2}:P_m&=&3I^2_2\frac{r’_2}{s}:3I^2_2r’_2:3I^2_2\frac{1-s}{s}r’_2\\ \\
&=&\frac{1}{s}:1:\frac{1-s}{s}\\ \\
&&　↓s倍する\\ \\
&=&1:s:(1-s)
\end{eqnarray}\)

となります。

　

関連記事

　

参考書