概要
Δ結線された電源と、Y結線された負荷の計算問題です。
Δ-Y変換と、フェーザ表示の二つを理解する必要があるので、三相交流回路の問題の中でも少し難しめかと思います。
キーワード
三相交流回路、Δ-Y変換、フェーザ表示
問題
図のように、相電圧200Vの対称三相交流電源に、複素インピーダンス\(Z=5\sqrt{3}+j5[Ω]\)の負荷がY結線された平衡三相負荷を接続した回路がある。
次の(a)及び(b)の問に答えよ。
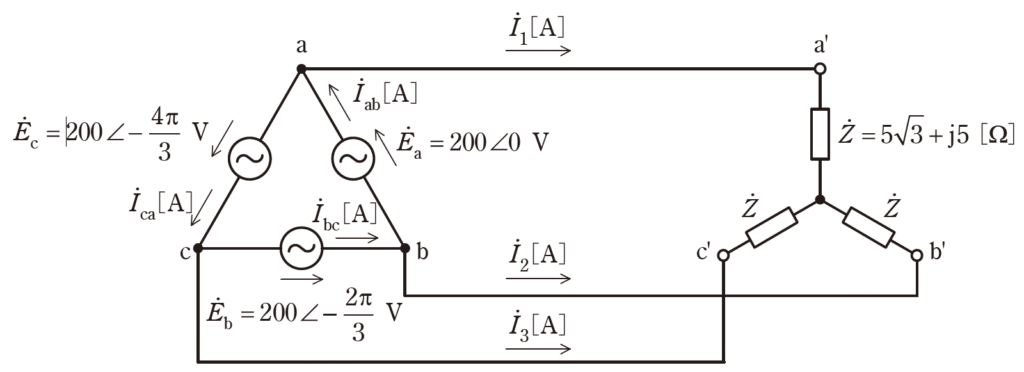
(a) 電流\(\dot{I}_1\)の値\([A]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)\(20.00∠-\frac{π}{3}\) (2)\(11.55∠-\frac{π}{3}\) (3)\(16.51∠-\frac{π}{6}\)
(4)\(20.00∠-\frac{π}{6}\) (5)\(11.55∠-\frac{π}{6}\)
(b) 電流\(\dot{I}_{ab}\)の値\([A]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)\(20.00∠-\frac{π}{6}\) (2)\(6.67∠-\frac{π}{6}\) (3)\(11.55∠-\frac{π}{6}\)
(4)\(6.67∠-\frac{π}{3}\) (5)\(11.55∠-\frac{π}{3}\)
答え
(a)(2)
(b)(2)
解説テキスト リンク
回答解説
(a)問題
回答の流れ
1.Δ結線の相電圧\(\dot{E}_{a}\)と線間電圧\(\dot{V}_{ab}\)の関係を確認する
2.Y結線の線間電圧\(\dot{V}_{ab}\)と、相電圧\(\dot{E}_{Ya}\)をベクトル図から導出する
3.三相負荷のインピーダンス\(\dot{Z}\)をフェーザ表示にする
4.線電流\(\dot{I}_1\)を求める
1.Δ結線の相電圧\(\dot{E}_{a}\)と線間電圧\(\dot{V}_{ab}\)の関係を確認する
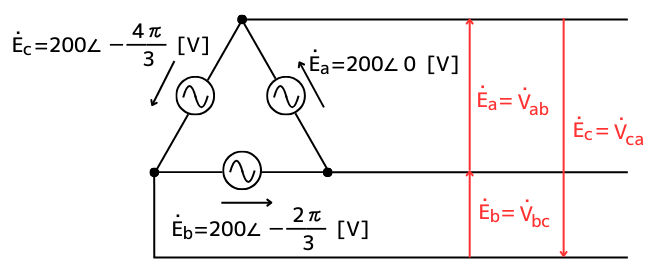
Δ結線の相電圧\(\dot{E}_a\)と線間電圧\(\dot{V}_{ab}\)は、電圧の大きさも、位相も等しいです。
2.Y結線の線間電圧\(\dot{V}_{ab}\)と、相電圧\(\dot{E}_{Ya}\)をベクトル図から導出する
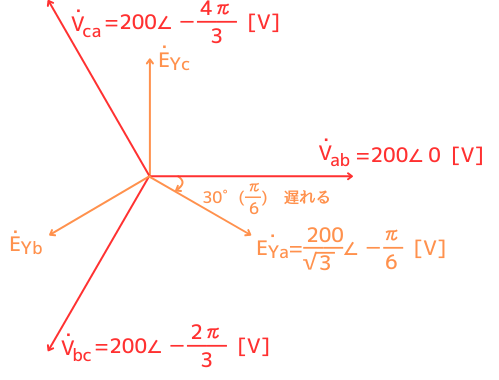
Y結線の線間電圧\(\dot{V}_{ab}\)と相電圧\(\dot{E}_{Ya}\)の関係は、
・相電圧の大きさは線間電圧の大きさの\(\frac{1}{\sqrt{3}}\)倍の大きさ
・相電圧の位相は、線間電圧から\(30°\)(\(\frac{π}{6}\))遅れている。
これをベクトル図に描くと、左図になります。
Y結線の線間電圧\(\dot{V}_{ab}\)も、Δ結線の相電圧\(\dot{E}_a\)と等しいので、
\(\dot{V}_{ab}=200∠0\)
Y結線の相電圧\(\dot{E}_{Ya}\)は、Y結線の線間電圧\(\dot{V}_{ab}\)の大きさの\(\frac{1}{\sqrt{3}}\)倍で、位相が\(30°\)(\(\frac{π}{6}\))遅れなので、
\(\dot{E}_{Ya}=\frac{200}{\sqrt{3}}∠-\frac{π}{6}\) …①
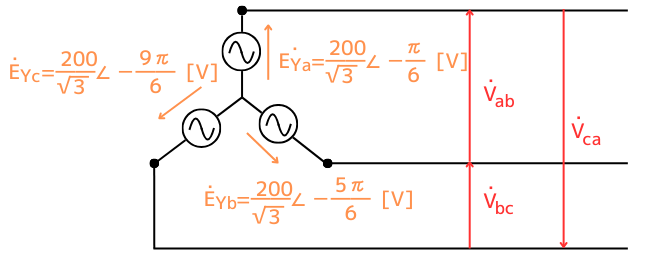
以上のことから、Y結線の線間電圧、相電圧を結線図に示すと、左図のようになります。
3.三相負荷のインピーダンス\(\dot{Z}\)をフェーザ表示にする
Y結線された三相負荷のインピーダンス(\(\dot{Z}=5\sqrt{3}+j5[Ω]\))をフェーザ表示に変換します。
インピーダンスの大きさ\(|\dot{Z}|\)は、
\(|\dot{Z}|=\sqrt{(5\sqrt{3})^2+5^2}=\sqrt{100}=10[Ω]\)
インピーダンスの位相角\(θ\)は、
\(θ=tan^{-1}\frac{Im(\dot{Z})}{Re(\dot{Z})}=tan^{-1}\frac{5}{5\sqrt{3}}=tan^{-1}\frac{1}{\sqrt{3}}\)
\(tanθ\)が\(\frac{1}{\sqrt{3}}\)となるような位相角\(θ\)は、30°(\(\frac{π}{6}\))のときです。
したがって、三相負荷のインピーダンス\(\dot{Z}\)をフェーザ表示すると、
\(\dot{Z}=|\dot{Z}|∠θ=10∠\frac{π}{6}\) …②
4.線電流\(\dot{I}_1\)を求める
線電流\(\dot{I}_1\)は、Y結線の相電圧\(\dot{E}_{Ya}\)と、三相負荷のインピーダンス\(\dot{Z}\)から、次式で表せます。
\(\dot{I}_1=\frac{\dot{E}_{Ya}}{\dot{Z}}=\frac{\frac{200}{\sqrt{3}}∠-\frac{π}{6}}{10∠\frac{π}{6}}=\frac{20}{\sqrt{3}}∠(-\frac{π}{6}-\frac{π}{6})=11.55∠-\frac{π}{3}\)
以上より、(a)問題は(2)\(11.55∠-\frac{π}{3}\) が答えです。
(b)問題
Y結線における線電流\(\dot{I}_1\)と、相電流\(\dot{I}_{ab}\)の関係は、
・相電流の大きさは、線電流の大きさの\(\frac{1}{\sqrt{3}}\)倍です。
・相電流の位相は、線電流の位相より30°(\(\frac{π}{6}\))進みです。
したがって、
\(\begin{eqnarray}
\dot{I}_{ab}&=&\frac{\dot{I}_1}{\sqrt{3}}∠\frac{π}{6} \\ \\
&=&\frac{11.55}{\sqrt{3}}∠(-\frac{π}{3}+\frac{π}{6}) \\ \\
&=&6.67∠-\frac{π}{6}
\end{eqnarray}\)
以上より、(b)問題は(2)\(6.67∠-\frac{π}{6}\) が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問15
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント