概要
交流回路に流れる電流を同相成分と、遅れ成分に分けて計算する問題です。
複素数平面上に成分を分わけて描くという解法が思い浮かぶか否かが鍵となり、難しい問題です。
キーワード
複素数平面
問題
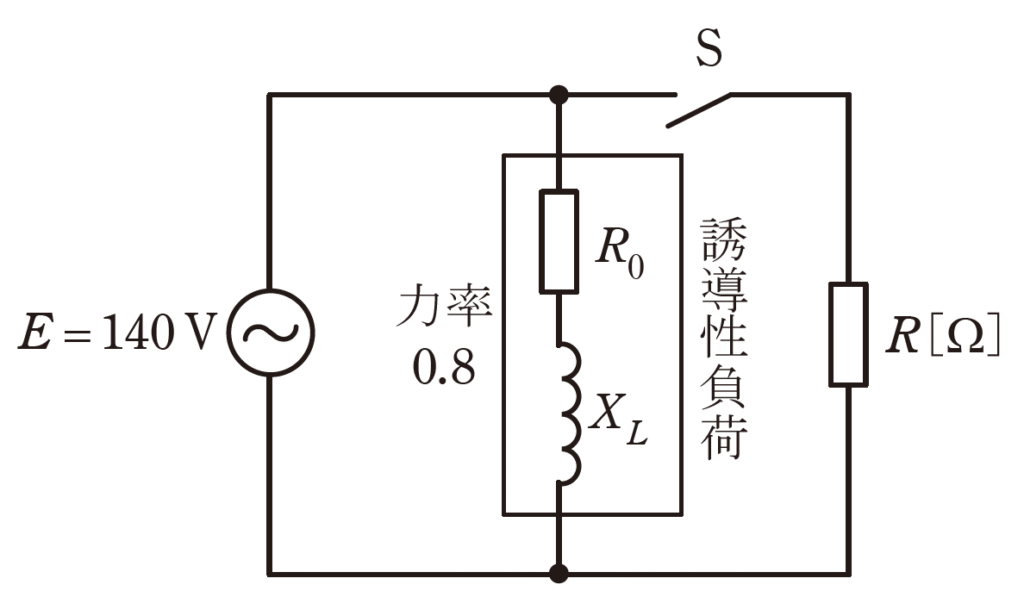
図の交流回路において、電源電圧を\(E=140V\)とする。
この電源に抵抗\(R_0[Ω]\)と誘導性リアクタンス\(X_L[Ω]\)とからなる力率\(0.8\)の誘導性負荷を接続したところ、電源から流れ出る電流の大きさは\(30A\)であった。
次に、スイッチSを閉じ、誘導性負荷と並列に抵抗\(R[Ω]\)を接続すると、電源から流れ出る電流の大きさが\(82A\)となった。
このとき、抵抗\(R[Ω]\)の大きさとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.5 (2) 2.3 (3) 2.5 (4) 2.9 (5) 3.0
答え
(1)
解説テキスト リンク
回答解説
回答の流れ
1. 誘導性負荷に流れる電流の同相成分、90°遅れ成分に分ける
2. 抵抗Rに流れる電流\(I_R\)を求める
3. 3平方の定理から抵抗\(R\)を求める
1. 誘導性負荷に流れる電流の同相成分、90°遅れ成分に分ける
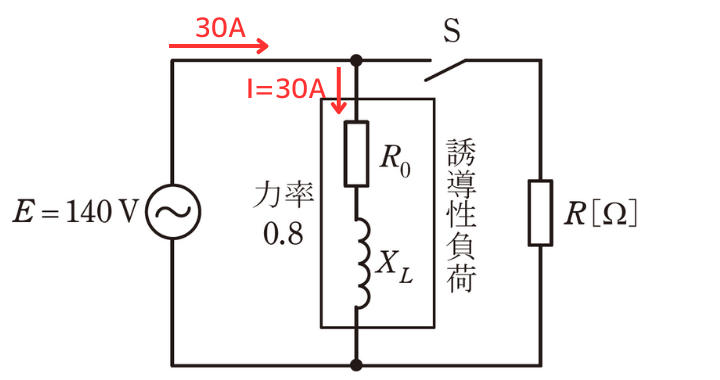
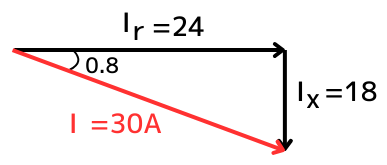
誘導性負荷に流れる電流\(30A\)のうち、同相成分\(I_r\)と、90°遅れ成分\(I_x\)に分けて考えます。力率は\(cosθ=0.8\)なので、
\(I_r=30cosθ=24A\)
\(I_x=30sinθ=18A\)
2. 抵抗Rに流れる電流\(I_R\)を求める
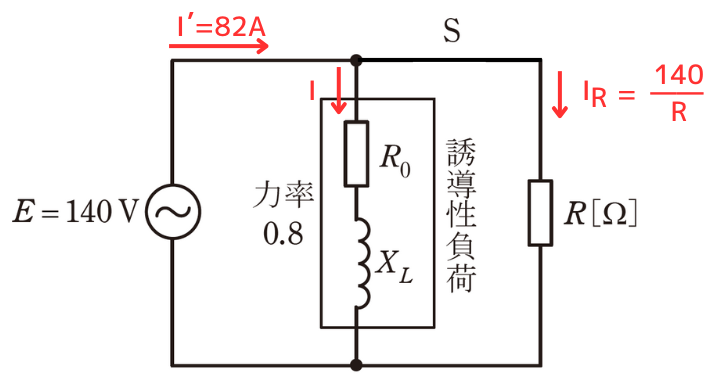
スイッチSを閉じて、抵抗Rに流れる電流を\(I_R\)とすると、
\(I_R=\frac{E}{R}=\frac{140}{R}[A]\)
3. 3平方の定理から抵抗\(R\)を求める
スイッチSを閉じた後の、電源から流れ出る電流を\(I’=82[A]\)とすると、次の三平方の定理の式が成り立ちます。
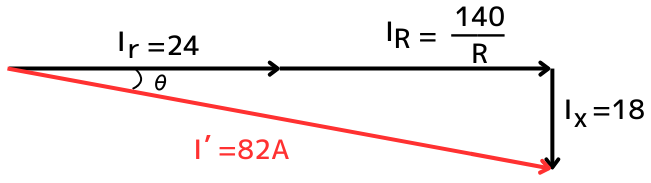
\(I’^2=(I_r+I_R)^2+I_x^2\)
⇔ \(82^2=(24+\frac{140}{R})^2+18^2\)
⇔ \(6724=(24+\frac{140}{R})^2+324\)
⇔ \((24+\frac{140}{R})^2=6400\)
⇔ \(24+\frac{140}{R}=80\)
⇔ \(R=\frac{140}{56}=2.5Ω\)
以上より、(3)2.5 が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問9
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント