難易度
平行平板コンデンサの論説問題で、少々ひねった問題で難しいです。
誘電率εが出てくる公式を丸暗記しているだけの場合は、引っかかりやすいです。
電界分布、電位分布、静電容量、静電エネルギー、電荷の各項目の意味をしっかりと捉えて回答しましょう。
問題
極板間が比誘電率\(ε_r\)の誘電体で満たされている平行平板コンデンサに一定の直流電圧が加えられている。このコンデンサに関する記述a~eとして、誤っているものの組合わせを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
a. 極板間の電界分布は\(ε_r\)に依存する。
b. 極板間の電位分布は\(ε_r\)に依存する。
c. 極板間の静電容量は\(ε_r\)に依存する。
d. 極板間に蓄えられる静電エネルギーは\(ε_r\)に依存する。
e. 極板上の電荷(電気量)は\(ε_r\)に依存する。
(1) a , b
(2) a , e
(3) b , c
(4) a , b , d
(5) c , d , e
答え
(1)
要点整理
電界の強さ\(E[V/m]\)について
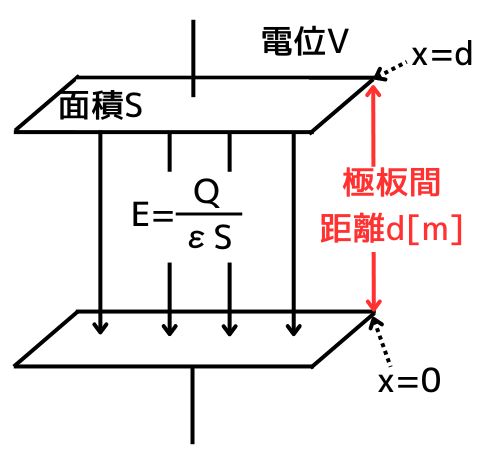 | 電界の強さ\(E\)は、 \(Q[C]\)の電荷が出す電気力線の本数は\(N=\frac{Q}{ε}[本]\)です。 電界の強さ\(E\)は、電気力線の本数の密度と等しいので、 \(\displaystyle E=\frac{N}{S}=\frac{Q}{εS}\) の式で表されます。 誘電率\(ε\)、比誘電率\(ε_r\)、真空の誘電率\(ε_0\)の関係は、 \(ε=ε_rε_0\) なので、 \(\displaystyle E=\frac{Q}{ε_rε_0S}\) となります。 |
電界と電圧の関係について
電界の強さ\(E\)と、電位\(V\)の関係は、\(V=Ed\)です。
\(V=Ed\)を導出します。
電位\(V\)は、1Cの電荷を基点から対象点へ動かすときの仕事です。
基点はコンデンサの上端で\(d[m]\)
対象点はコンデンサの下端で\(0[m]\)
としたとき、電界の強さ\(E\)と電位\(V\)の関係は次のように表されます。
\(\displaystyle V=-\int_d^0E・dr=-\int_d^0\frac{Q}{εS}dr=-\frac{Q}{εS}[r]_d^0=\frac{Q}{εS}d=Ed\)
以上より、\(V=Ed\)が導出できました。
電界分布について
電界分布は、電界の強さ\(E\)が場所によってどのように変化するかを示したものです。
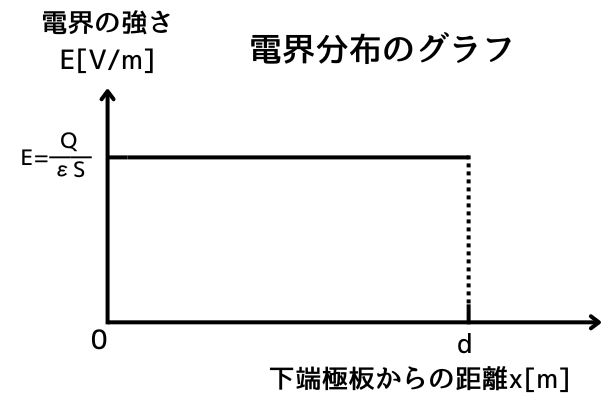 | 電界分布は、コンデンサ内の電界の強さ\(E\)が、どのように分布しているかを示します。 極板間距離が\(d[m]\)のコンデンサの ・下端の極板の位置を\(0[m]\) ・下端の極板からの距離を\(x[m]\) ・上端の極板の位置を\(d[m]\) とします。 この時、下端の極板からの距離に応じた電界の強さ\(E\)をグラフにしたとき、電界分布のグラフに示した通り、常に一定の値\(E=\frac{Q}{εS}\)を示すグラフになります。 |
電位分布について
電位\(V\)と、電界の強さ\(E\)の関係は、\(V=Ed\)です。
電位分布は常に一定の値を示しますので、電位分布のグラフを描くと下図のようになります。
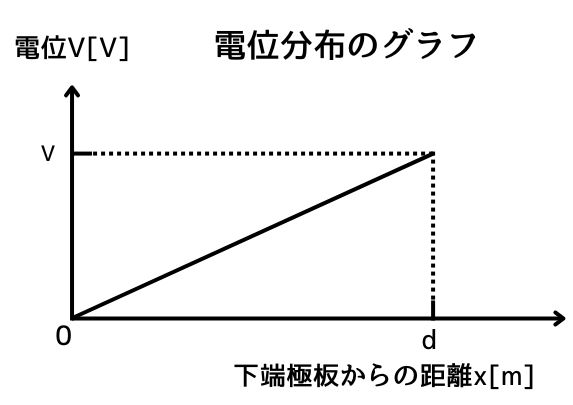
距離\(x\)に応じて、電位は直線的に増加します。
静電容量\(C[F]\)について
静電容量の式を導出します。
誘電率を\(ε[F/m]\)、真空の誘電率を\(ε_0[F/m]\)、誘電体の比誘電率を\(ε_r\)
極板面積を\(S[m^2]\)、極板間距離を\(d[m]\)とします。
静電容量は単位電圧あたりの蓄えられた電荷として与えられるので
\(\displaystyle C=\frac{Q}{V}\) ………①
です。
\(\displaystyle E=\frac{Q}{εS}\) ………②
\(V=Ed\) ………③
\(ε=ε_rε_0\) ………④
なので、①に②③④を代入すると、
\(\displaystyle C=\frac{Q}{V}=\frac{εS}{d}=ε_rε_0\frac{S}{d}\)
以上より、
\(\displaystyle C=ε_rε_0\frac{S}{d}\)
です。
静電エネルギー\(U[J]\)について
静電エネルギーの式
\(\displaystyle U=\frac{1}{2}CV^2\)
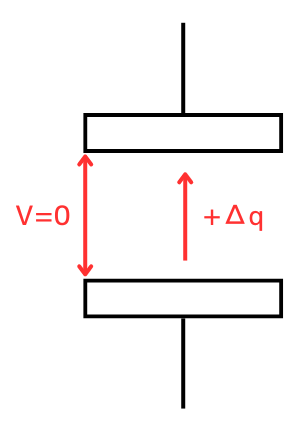
電位が\(V\)だけ大きいところに微小電荷\(Δq\)を動かすには、\(Δq・V\)の仕事が必要になります。
コンデンサ内に電荷が無い時、\(Δq\)を移動させるエネルギーは、\(V=0[V]\)なので、必要な仕事量\(ΔW_0=0[J]\)です。
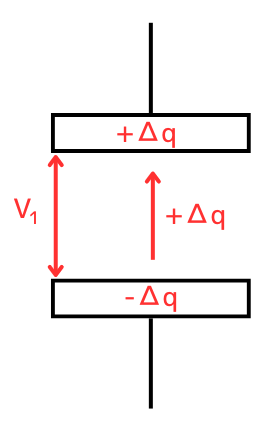
しかし、電荷を移動させていくと、\(\displaystyle V=\frac{q}{C}\)の関係から、電位差も大きくなっていきますので、必要な仕事量が増加していきます。
\(Δq\)が移動し、コンデンサの電位が\(V_1[V]\)になった時、次に\(Δq\)を移動させるエネルギーは、\(ΔW_1=ΔqV_1\)です。
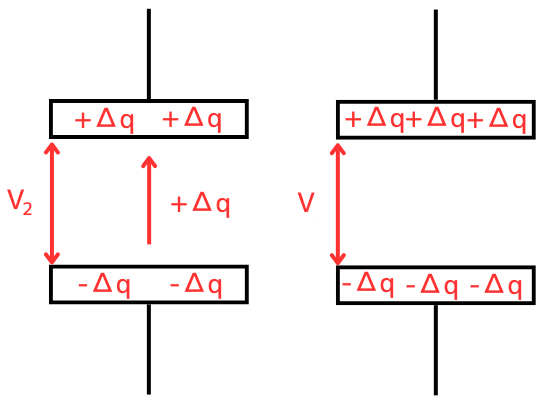
\(Δq\)が移動し、コンデンサの電位が\(V_2[V]\)になった時、
次に\(Δq\)を移動させるエネルギーは、\(ΔW_2=ΔqV_2\)と進んでいきます。
最終的に、電位\(V[V]\)になったとき、
電荷の移動がなくなったとします。
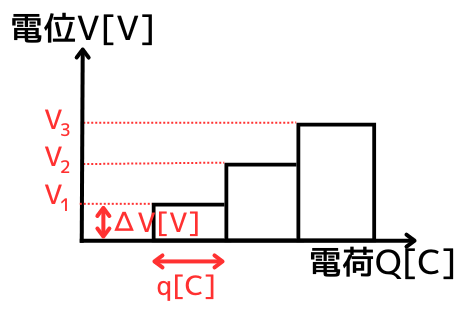
今までの微小電荷\(q[C]\)の溜まりと、コンデンサの電位\(V[V]\)の変化をグラフにすると、左図のようになります。
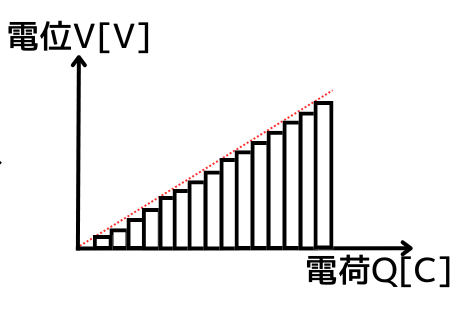
横軸をもっと細かくしていくと、直線グラフを描くことができます。
コンデンサは、\(q=0\)から、\(q=Q\)まで電荷を蓄えるので、エネルギー\(ΔW=ΔqV\)の式を、電荷が\(Q=0[C]\)から、\(Q=Q[C]\)になるまで積分することで、コンデンサに蓄えられる静電エネルギーが求められます。
\(q=CV\)の式から、電位Vの式は、\(\displaystyle V=\frac{q}{C}\)です。
これを微小電荷\(Δq\)のエネルギー\(ΔW\)の式に代入すると、
\(\displaystyle ΔW=V・Δq=\frac{q}{C}Δq\)
静電エネルギー\(U[J]\)を求めるため、\(ΔW\)を積分すると、
\(\displaystyle U=\int_0^Q ΔW=\int_0^Q \frac{q}{C}dq=\left[ \frac{q^2}{2C} \right]_0^Q=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}CV^2 \)
以上より、
\(\displaystyle U=\frac{1}{2}CV^2\)
が求まりました。
極板上の電荷\(Q[C]\)について
極板上に蓄えられる電荷は、
\(Q=CV\)
です。
要点整理の適用
(a)
電界の強さ\(E\)は\(\displaystyle E=\frac{Q}{ε_rε_0S}\)のため、比誘電率\(ε_r\)依存するとしたくなりますが、これは間違いです。
極板間が比誘電率\(ε_r\)の誘電体で満たされているコンデンサにおいて、電界の強さ\(E\)は\(V=Ed\)の関係式があります。
問題の条件から、一定の直流電圧\(V\)が与えられているので、電界の強さ\(E\)は比誘電率\(ε_r\)に依存しません。そのため、電界分布も比誘電率\(ε_r\)に依存しません。
したがって、誤っています。
(b)
問題の条件から、一定の直流電圧\(V\)が与えられているので、比誘電率\(ε_r\)に依存しません。
そのため、電位分布も比誘電率\(ε_r\)に依存しません。
したがって、誤っています。
(c)
静電容量\(C\)は、\(\displaystyle C=ε_rε_0\frac{S}{d}\)です。
そのため、静電容量\(C[F]\)は、比誘電率\(ε_r\)に比例して大きくなります。
したがって、正しいです。
(d)
静電エネルギー\(U\)は、\(\displaystyle U=\frac{1}{2}CV^2\)です。
静電容量\(C\)は比誘電率\(ε_r\)に比例します。
電圧\(V\)は問題の条件から、比誘電率\(ε_r\)に依存しません。
そのため、静電エネルギー\(U\)は、比誘電率\(ε_r\)に比例して大きくなります。
したがって、正しいです。
(e)
極板上に蓄えられる電荷\(Q\)は、\(Q=CV\)です。
静電容量\(C\)は比誘電率\(ε_r\)に比例します。
電圧\(V\)は問題の条件から、比誘電率\(ε_r\)に依存しません。
そのため、極板上に蓄えられる電荷\(Q\)は、比誘電率\(ε_r\)に比例して大きくなります。
したがって、正しいです。
以上より、
誤っているものの組合わせは、(1) a , b です。
出典元
令和5年度第三種電気主任技術者試験 理論科目A問題下期問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント