概要
環状鉄心の2つのコイルの自己インダクタンスから巻き数を計算する問題です。
いくつか解答アプローチはありますが、いずれにしても自己インダクタンス周りの計算方法について理解を求められます。
キーワード
環状鉄心、自己インダクタンス
問題
図のように、環状鉄心に二つのコイルが巻かれている。
コイル1の巻数は\(N\)であり、その自己インダクタンスは\(L[H]\)である。
コイル2の巻数は\(n\)であり、その自己インダクタンスは\(9L[H]\)である。
巻数nの値を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、鉄心は均一で一定断面積をもち、コイル及び鉄心の漏れ磁束はなく、鉄心の磁気飽和もないものとする。
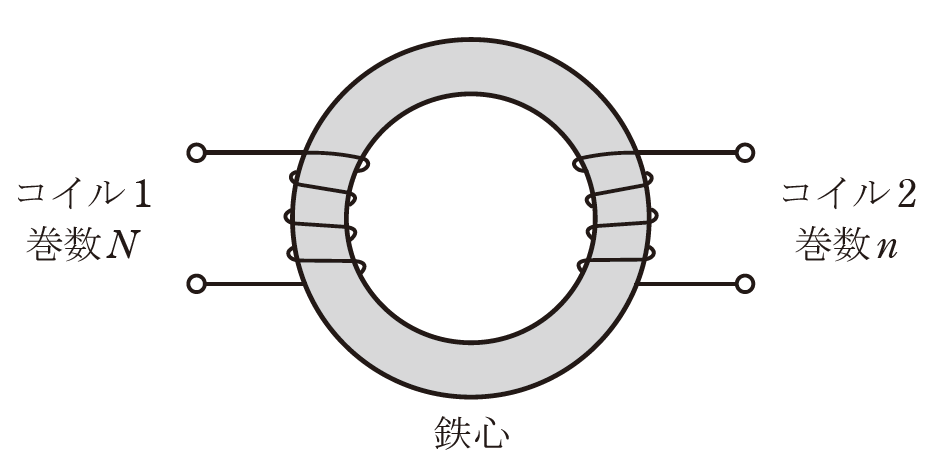
(1) \(\frac{N}{9}\) (2) \(\frac{N}{3}\) (3) \(3N\) (4) \(9N\) (5) \(81N\)
答え
(3)
解説テキスト リンク
回答解説
1. 磁束と自己インダクタンスの関係から磁束\(Φ\)の式を求める
2. 磁束\(Φ\)を磁気回路のパラメータで表す
3. 1.と2.で求めた式から、自己インダクタンスの式を求める
4. コイル1とコイル2の自己インダクタンスから巻き数を求める
1. 磁束と自己インダクタンスの関係から磁束\(Φ\)の式を求める
磁束と自己インダクタンスの関係は、
\(NΦ=LI\)
⇔ \(Φ=\frac{LI}{N}\) …①
です。
2. 磁束\(Φ\)を磁気回路のパラメータで表す
鉄心の断面積\(S[m^2]\)、鉄心内の磁束密度が\(B[T]\)としたとき、
鉄心内の磁束\(Φ[Wb]\)は、
\(Φ=BS\) …②
鉄心の透磁率を\(μ[H/m]\)、磁界強度\(H[A/m]\)とすると、鉄心内の磁束密度\(B[T]\)は、
\(B=μH\) …③
コイルの作り出す起磁力\(F[A]\)は、平均磁路長を\(l[m]\)としたとき、
\(F=NI=Hl\)
⇔ \(H=\frac{NI}{l}\) …④
②式に③・④を代入していくと、
\(Φ=BS=μHS=\frac{μNIS}{l}\) …⑤
となります。
3. 1.と2.で求めた式から、自己インダクタンスの式を求める
①・⑤式から、
\(\frac{LI}{N}=\frac{μNIS}{l}\)
⇔ \(L=\frac{μN^2S}{l}\) …⑥
4. コイル1とコイル2の自己インダクタンスから巻き数を求める
⑥式から、自己インダクタンス\(L\)は、コイルの巻き数\(N\)の二乗に比例することがわかります。
コイル1は、
\(L=\frac{μN^2S}{l}\) …⑦
コイル2は、
\(9L=\frac{μn^2S}{l}\) …⑧
⑧÷⑦式とすると、
\(\frac{9L}{L}=9=\frac{n^2}{N^2}\)
⇔ \(n^2=9N^2\)
⇔ \(n=3N\)
以上より、(3)\(3N\) が答えです。
別解
自己インダクタンス\(L[H]\)に蓄えられるエネルギー\(U[J]\)は、
\(U=\frac{1}{2}LI^2\)
です。
コイル及び鉄心の漏れ磁束がないとしたとき、コイル1、コイル2に蓄えられる磁気エネルギーは同じです。
コイル1の自己インダクタンスは\(L[H]\)、コイル2の自己インダクタンスは\(9L[H]\)なので、コイル1の電流を\(I_1\)、コイル2の電流を\(I_2\)とすると、
\(U=\frac{1}{2}LI_1^2=\frac{1}{2}9LI_2^2\)
⇔ \( I_1=3I_2\)
磁束の漏れはないので、コイル1・2の磁束鎖交数\(NΦ\)は同じです。したがって、
\(NΦ=LI_1=3LI_2\)
⇔ \(Φ=\frac{3LI_2}{N}\)
\(nΦ=9LI_2\)
⇔ \(n=\frac{9LI_2}{Φ}=3N\)
以上より、(3)\(3N\) が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問3
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント