概要
二(個の)電力計(で測定する方)法の名前通り、2個の単相電力計で三相交流の電力測定をすることが出来る方法です。
長所
・線間電圧と線電流を測定することで、三相交流の電力が測定できる。
・電力計が2つで三相交流を測定することが出来る。
・三相不平衡負荷でも測定が可能。
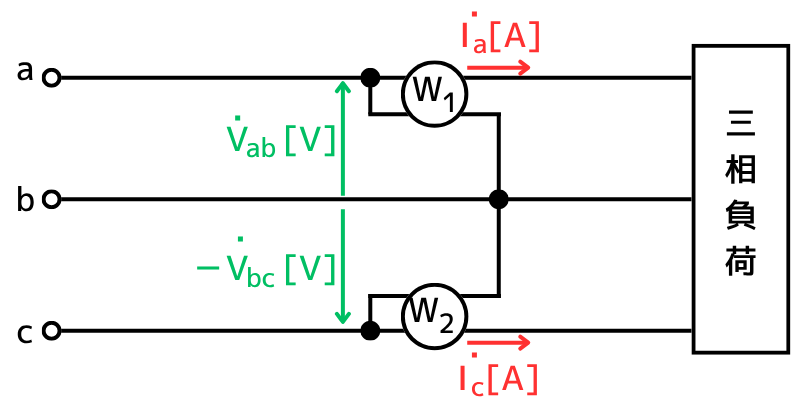
原理
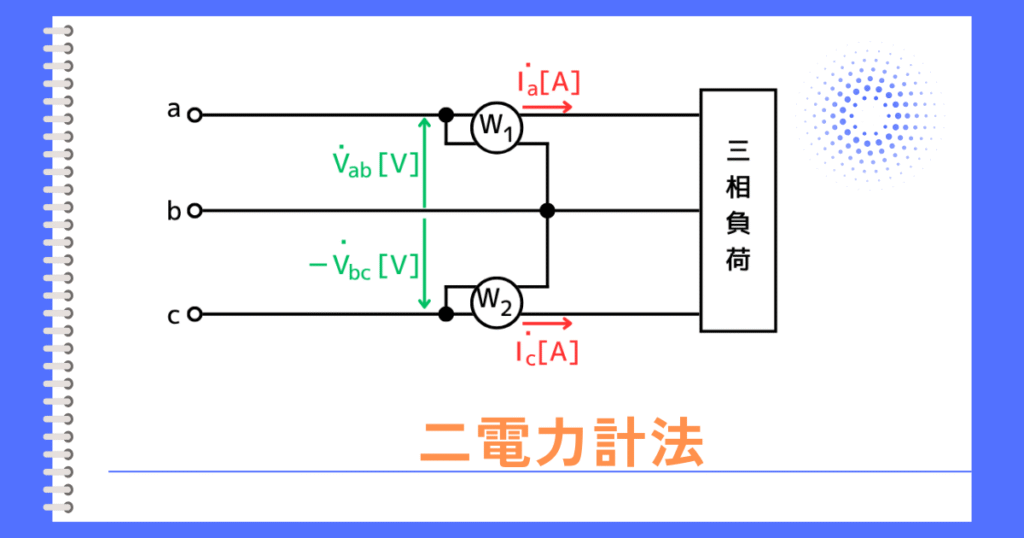
三相交流回路の各電圧、電流を左図に表します。
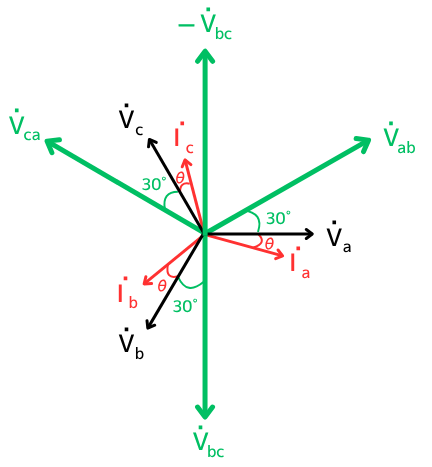
・相電圧:\(\dot{V}_a\)、\(\dot{V}_b\)、\(\dot{V}_c\)
・相電流:\(\dot{I}_a\)、\(\dot{I}_b\)、\(\dot{I}_c\)
・線間電圧:\(\dot{V}_{ab}\)、\(\dot{V}_{bc}\)、\(\dot{V}_{ca}\)
・相電圧と相電流の位相差角:\(θ\)
\(W_2\)電力計の極を逆に接続するため、線間電圧は\(-\dot{V}_{bc}\)も記載します。
計算に使用するベクトルだけ取り出します。
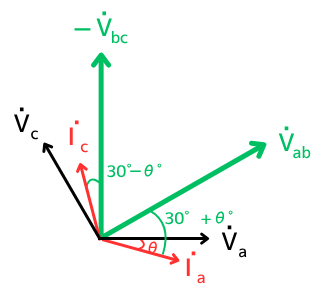
電力計\(W_1\)、\(W_2\)の測定内容は次のようになります。
\(\begin {eqnarray}
W_1&=&\dot{V}_{ab}・\dot{I}_a \\
&=&VIcos(30°+θ) \\
&=&VI(cos30°cosθ-sin30°sinθ) \\
&=&VI(\frac{\sqrt{3}}{2}cosθ-\frac{1}{2}sinθ) \\
\end{eqnarray}\)
\(\begin {eqnarray}
W_2&=&\dot{-V}_{bc}・\dot{I}_c \\
&=&VIcos(30°-θ) \\
&=&VI(cos30°cosθ+sin30°sinθ) \\
&=&VI(\frac{\sqrt{3}}{2}cosθ+\frac{1}{2}sinθ) \\
\end{eqnarray}\)
\(V\):線間電圧の大きさ
\(I\):線電流の大きさ
参考:加法定理
\(cos(α+β)=cosαcosβ-sinαsinβ\)
\(cos(α-β)=cosαcosβ+sinαsinβ\)
有効電力\(P[W]\)の計算
\(\begin {eqnarray}
P&=&W_1+W_2 \\
&=&VI(\frac{\sqrt{3}}{2}cosθ-\frac{1}{2}sinθ)+VI(\frac{\sqrt{3}}{2}cosθ+\frac{1}{2}sinθ) \\
&=&\sqrt{3}VIcosθ
\end{eqnarray}\)
したがって、有効電力が求まりました。
無効電力\(Q[Var]\)の計算
\(\begin {eqnarray}
Q&=&W_2-W_1 \\
&=&VI(\frac{\sqrt{3}}{2}cosθ+\frac{1}{2}sinθ)-VI(\frac{\sqrt{3}}{2}cosθ-\frac{1}{2}sinθ) \\
&=&VIsinθ
\end{eqnarray}\)
力率\(cosθ\)の計算
\(P=W_1+W_2=\sqrt{3}VIcosθ\)
⇔ \(\displaystyle cosθ=\frac{W_1+W_2}{\sqrt{3}VI}\)
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント